
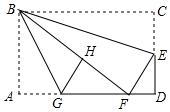
 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:分析 根据矩形的性质得出∠A=∠C=∠D=∠ABC=90°,AB=CD=6,BC=AD=10,根据折叠得出∠BAG=∠FBG,∠CBE=∠FBE,AG=GH,BC=BF=10,AB=BH=6,根据勾股定理求出AG=GH=3,再逐个判断即可.
解答 解:∵根据折叠得出∠BAG=∠FBG,∠CBE=∠FBE,
又∵四边形ABCD是矩形,
∴∠BAC=90°,
∴∠EBG=$\frac{1}{2}×90°=45°$,∴①正确;
∵四边形ABCD是矩形,
∴AB=DC=6,BC=AD=10,∠A=∠C=∠D=90°,
∴根据折叠得∠BFE=∠C=90°,
∴∠ABG+∠BGA=90°,∠EFD+∠BFA=90°,
∵∠BGA>∠BFA,
∴∠BAG≠∠EFD,
∵∠GHB=∠A=90°,∠EFB=∠C=90°,
∴∠GHB=∠EFB,
∴GH∥EF,
∴∠EFD=∠HGF,
根据已知不能推出∠AGB=∠HGF,
∴∠AGB≠∠EFD,
即△DEF和△ABG不全等,∴②错误;
∵根据折叠得:AB=BH=6,BC=BF=10,
∴由勾股定理得:AF=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴DF=10-8=2,HF=10-6=4,
设AG=HG=x,
在Rt△FGH中,由勾股定理得:GH2+HF2=GF2,
即x2+42=(8-x)2,
解得:x=3,
即AG=HG=3,
∴S△ABG=$\frac{1}{2}×AB×AG$=$\frac{1}{2}×6×3$=9,S△FHG=$\frac{1}{2}×GH×HF$=$\frac{1}{2}×3×4$=6,∴③错误;
∵AG+DF=3+2=5,GF=10-3-2=5,∴④正确;
故答案为:①④.
点评 本题考查了勾股定理,折叠的性质,矩形的性质等知识点,能灵活运用定理进行推理和计算是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 978×103 | B. | 97.8×104 | C. | 9.78×105 | D. | 0.978×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com