
如图在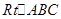 中,
中,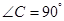 ,
,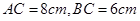 ,点P以
,点P以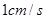 的速度从A开始沿着折线
的速度从A开始沿着折线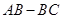 运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;
运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;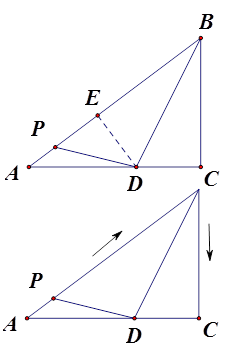
(1)直接写出AB的长度;
(2)把 沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
(3)若点D在(2)中的位置,当t为几秒时,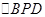 为直角三角形?
为直角三角形?
(1) ;(2)
;(2) ;(3)
;(3)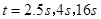
解析试题分析:(1)在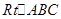 中,根据勾股定理可求得AB的长度;
中,根据勾股定理可求得AB的长度;
(2)设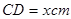 ,由折叠可知:
,由折叠可知: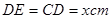 ,
, ,即可得到AE的长,表示出AD的长,在Rt△ADE中,根据勾股定理可得到关于x的方程,解出即可;
,即可得到AE的长,表示出AD的长,在Rt△ADE中,根据勾股定理可得到关于x的方程,解出即可;
(3)分 、
、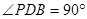 、
、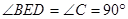 三种情况讨论,再结合勾股定理即可求得结果。
三种情况讨论,再结合勾股定理即可求得结果。
(1)
(2)设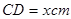
由折叠(轴对称)可知: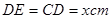 ,
,
∴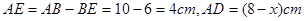
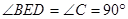 ,即
,即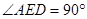
由勾股定理得: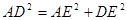
即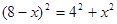
解得: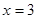
∴此时CD的长为 .
.
(3)当点P运动到(2)中的点E处时,即
此时PE=AE=4 ,
,
当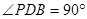 时
时
∵ ,
, ,
,

由勾股定理得: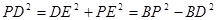
而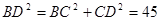
即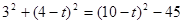
解得: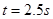 (经检验符合题意)
(经检验符合题意)
当点P运动到点C时,即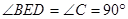
此时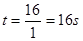
综上所述:当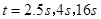 时△PBD为直角三角形.
时△PBD为直角三角形.
考点:本题考查的是勾股定理的应用,直角三角形的性质
点评:对于折叠问题,主要观察折叠前后的对应的角或边;对于直角三角形要考虑哪个角可以作为直角,哪一条边是直角边,哪一条边是斜边,同时熟练掌握勾股定理。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建晋江养正中学八年级上学期期中考试数学试题(解析版) 题型:解答题
如图在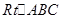 中,
中, ,
, ,点P以
,点P以 的速度从A开始沿着折线
的速度从A开始沿着折线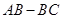 运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;
运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;

(1)直接写出AB的长度;
(2)把 沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
(3)若点D在(2)中的位置,当t为几秒时, 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源:江苏省期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
如图在![]() 中,
中,![]() ,
,![]() ,点P以
,点P以![]() 的速度从A开始沿着折线
的速度从A开始沿着折线![]() 运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;
运动到点C,点D在AC上,连接BD,PD,设点P的运动时间为t秒;
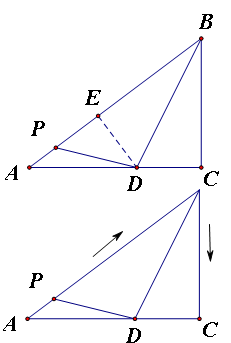
(1)直接写出AB的长度;
(2)把![]() 沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
沿着BD对折,点C恰好落在AB上的点E处,求此时CD的长;
(3)若点D在(2)中的位置,当t为几秒时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com