
【题目】已知△ABC, ①如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+ ![]() ∠A;
∠A;
②如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°﹣∠A;
③如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣ ![]() ∠A.
∠A.
上述说法正确的个数是( )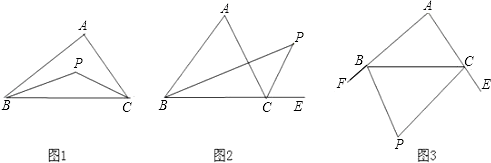
A.3个
B.2个
C.1个
D.0个
【答案】C
【解析】解:①若P点是∠ABC和∠ACB的角平分线的交点, 则∠PBC= ![]() ∠ABC,∠PCB=
∠ABC,∠PCB= ![]() ∠ACB
∠ACB
则∠PBC+∠PCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)
(180°﹣∠A)
在△BCP中利用内角和定理得到:
∠P=180﹣(∠PBC+∠PCB)=180﹣ ![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+ ![]() ∠A,
∠A,
故成立;
②当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
③若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC= ![]() ∠FBC=
∠FBC= ![]() (180°﹣∠ABC)=90°﹣
(180°﹣∠ABC)=90°﹣ ![]() ∠ABC,
∠ABC,
∠BCP= ![]() ∠BCE=90°﹣
∠BCE=90°﹣ ![]() ∠ACB
∠ACB
∴∠PBC+∠BCP=180°﹣ ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°﹣∠A
∴∠PBC+∠BCP=90°+ ![]() ∠A,
∠A,
在△BCP中利用内角和定理得到:
∠P=180﹣(∠PBC+∠PCB)=180﹣ ![]() (180°+∠A)=90°﹣
(180°+∠A)=90°﹣ ![]() ∠A,
∠A,
故成立.
∴说法正确的个数是2个.
故选C.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③周长相等的两个圆是等圆;④同圆中等弦所对的圆周角相等.其中正确的有 ( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )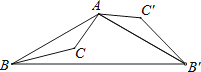
A.45°
B.60°
C.70°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕顶点C逆时针旋转得到△A′B′C , 且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )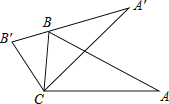
A.30°
B.35°
C.40°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC于E、F点. 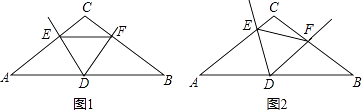
(1)如图1,若EF∥AB.求证:DE=DF. 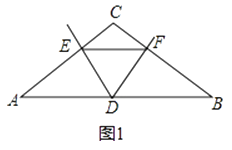
(2)如图2,若EF与AB不平行. 则问题(1)的结论是否成立?说明理由. 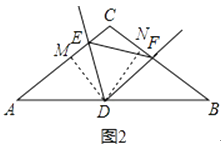
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和点B相距60cm,且关于直线L对称,一只电动青蛙在与直线L相距20cm,与点A相距50cm的点P1处以A为对称中心跳至P2处,然后从P2处以L为对称轴跳至P3处,再从P3处以B为对称中心跳至P4处,再从P4处以L为对称轴跳至P5处,又从P5处以A为对称中心跳至P6处…,如此重复跳跃,则P2011与直线L的距离是( )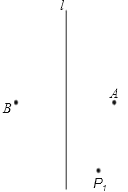
A.20cm
B.30cm
C.40cm
D.50cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com