
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OBn-1BnCn的顶点Bn的坐标是当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0)..
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OBn-1BnCn的顶点Bn的坐标是当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0).. 分析 首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标之间的规律,然后根据规律计算出点Bn的坐标.
解答 解:∵边长为1的正方形OA1B1C1的两边在坐标轴上,
∴B1点坐标为(1,1),OB1=$\sqrt{2}$,
∵正方形OB1B2C2是正方形OA1B1C1的对角线OB为边,
∴OB2=2,
∴B2点坐标为(0,2),
同理可知OB3=2$\sqrt{2}$,B3点坐标为(-2,2),
同理可知OB4=4,B4点坐标为(-4,0),
B5点坐标为(-4,-4),B6点坐标为(0,-8),
B7(8,-8),B8(16,0),B9(16,16),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的$\sqrt{2}$倍,
∴当k为自然数,
如果n=8k+1时,那么Bn(24k,24k);
如果n=8k+2时,那么Bn(0,24k+1);
如果n=8k+3时,那么Bn(-24k+1,24k+1);
如果n=8k+4时,那么Bn(-24k+2,0);
如果n=8k+5时,那么Bn(-24k+2,-24k+2);
如果n=8k+6时,那么Bn(0,-24k+3);
如果n=8k+7时,那么Bn(24k+3,-24k+3);
如果n=8k+8时,那么Bn(24k+4,0).
故答案为:当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0).
点评 本题主要考查正方形的性质,规律型:点的坐标以及分类讨论思想,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的$\sqrt{2}$倍,此题难度较大.


科目:初中数学 来源: 题型:选择题
 如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )
如图,∠ACD为△ABC的一个外角,∠ABC与∠ACD的平分线交于E点,∠A与∠E的关系为( )| A. | ∠E=90°+$\frac{1}{2}$∠A | B. | ∠E=90°-$\frac{1}{2}$∠A | C. | ∠E=$\frac{1}{2}$∠A | D. | ∠E=2∠A |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
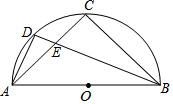 如图,AB是半圆O的直径,C是$\widehat{AB}$的中点,D是$\widehat{AC}$的中点,AC与BD相交于点E.
如图,AB是半圆O的直径,C是$\widehat{AB}$的中点,D是$\widehat{AC}$的中点,AC与BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com