
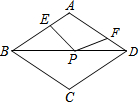
 如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作F点关于BD的对称点F′,则PF=PF′,由两点之间线段最短可知当E、P、F′在一条直线上时,EP+FP有最小值,然后求得EF′的长度即可.
解答 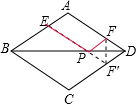 解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
点评 本题主要考查的是菱形的性质、轴对称--路径最短问题,明确当E、P、F′在一条直线上时EP+FP有最小值是解题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (a+b)2=a2+b2 | C. | (-a)3=-6a3 | D. | -(x-2)=2-x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
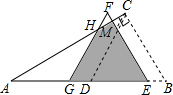 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.| A. | $\frac{7\sqrt{3}}{8}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )
某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )| A. | 16,15 | B. | 15,15.5 | C. | 15,17 | D. | 15,16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 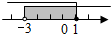 | B. | 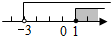 | C. | 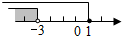 | D. | 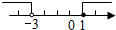 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com