
 已知:如图,AB,AC是⊙O的切线,B,C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB,AC分别交于点D,E.
已知:如图,AB,AC是⊙O的切线,B,C是切点,过$\widehat{BC}$上的任意一点P作⊙O的切线与AB,AC分别交于点D,E.分析 (1)连接OB,OC,OD,OP,OE,根据切线长定理得到OD平分∠BOP,OE平分∠POC,计算即可;
(2)根据圆周角定理得到∠BOD=∠COE,证明△BOD≌△COE,得到OD=OE,根据等腰三角形三线合一证明结论.
解答 解:(1)连接OB,OC,OD,OP,OE,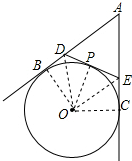
∵AB,AC,DE分别与⊙O相切,OB,OC,OP是⊙O的半径,
∴OB⊥AB,OC⊥AC,OP⊥DE,DB=DP,EP=EC,AB=AC,
∴∠OBA=∠OCA=90°,
∵∠A=50°,
∴∠BOC=360°-90°-90°-50°=130°,
∵OB⊥AB,OP⊥DE,DB=DP,
∴OD平分∠BOP,
同理得:OE平分∠POC,
∴∠DOE=∠DOP+∠EOP=$\frac{1}{2}$(∠BOP+∠POC)=$\frac{1}{2}$∠BOC=65°;
(2)当点P在$\widehat{BC}$的中点时,PD=PE,
∵P在$\widehat{BC}$的中点,
∴∠BOD=∠COE,
∴△BOD≌△COE,
∴OD=OE,又∠POD=∠POE,
∴PD=PE.
点评 本题考查的是切线长定理和切线的性质,掌握从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角是解题的关键.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
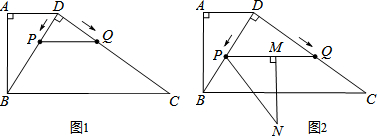
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
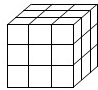 将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:
将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,若DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,求$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$.
如图所示,若DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,求$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
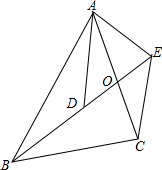 如图,四边形ABCE中,AC与BE交于点O,D是BO上一点,已知AD=4,△ABD∽△ACE.
如图,四边形ABCE中,AC与BE交于点O,D是BO上一点,已知AD=4,△ABD∽△ACE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com