
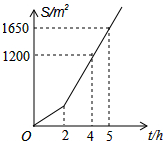
 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2.
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2. 分析 先利用待定系数法求出t≥2时,绿化面积S关于时间t的函数解析式,据此得出t=2时S的值,根据其实际意义即可得出答案.
解答 解:设t≥2时,绿化面积S关于时间t的函数解析式为S=kt+b,
将(4,1200)、(5,1650)代入,得:
$\left\{\begin{array}{l}{4k+b=1200}\\{5k+b=1650}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=450}\\{b=-600}\end{array}\right.$,
∴t≥2时,S=450t-600,
当t=2时,S=300,即工作2小时,绿化组完成绿化面积300m2,
∴该绿化组提高工作效率前每小时完成的绿化面积是$\frac{300}{2}$=150m2,
故答案为:150.
点评 本题主要考查一次函数的应用,熟练掌握待定系数法求函数解析式及理解函数图象各点的实际意义是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
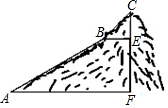 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
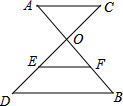 如图,AB、CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为$\frac{16}{3}$.
如图,AB、CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/cm | 180 | 180 | 185 | 185 |
| 方差 | 8.2 | 3.9 | 7.5 | 3.9 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com