Question

14．如图，在矩形ABCD中，BC=4，CD=3，直线MN过点A，∠BAN=∠DBC，点P是直线MN上的一个动点（不与点A重合），点E在射线AD上，满足∠PBE=∠BDC，设PA=x，
（1）如图①，若点P在射线AN上．求线段DE的长（用含x的代数式表示）并直接写出x的取值范围；
（2）如图②．若点P在射线AM上，求$\frac{BP}{EP}$的值；
（3）设直线PE交直线AB于点F，是否存在x的值，使△PAF为等腰三角形？若存在，直接写出x的值：若不存在，请说明理由．

Answer 1

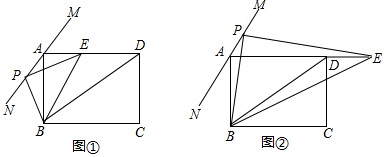
分析 （1）如图①中，作BF⊥AN于F．只要证明△ABP∽△DBE，可得$\frac{PA}{ED}$=$\frac{AB}{DB}$，即$\frac{x}{DE}$=$\frac{3}{5}$，由此即可解决问题．
（2）只要证明△ABD∽△PBE，可得$\frac{AB}{PB}$=$\frac{AD}{EP}$，推出$\frac{PB}{EP}$=$\frac{AB}{AD}$=$\frac{3}{4}$．
（3）①如图①中，当FA=FP时，由△ABE∽△ADB，可得BA²=AE•AD，求出DE即可解决问题．
②如图③当AP=AF时，只要证明EB=EF即可解决问题．

解答 解：（1）如图①中，作BF⊥AN于F．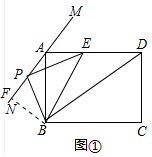

∵四边形ABCD是矩形，
∴∠BAD=∠AFB=90°，
∵∠ABF+∠BAF=90°，∠ADB+∠ABD=90°，∠BAF=∠ADB，
∴∠ABF=∠ABD=∠PBE，
∴∠PBF=∠ABE，
∴△PBF∽△EBA，
∴$\frac{PB}{BE}$=$\frac{BF}{BA}$，∴∠BPF=∠AEB，∠APB=∠BED，
∴$\frac{PB}{BF}$=$\frac{BE}{AB}$，∵∠ABF=∠PBE，
∴△ABF∽△EBP，
∴∠EPB=∠AFB=90°=∠BAE，
∵∠ABP=∠EBD，∠APB=∠BED，
∴△ABP∽△DBE，
∴$\frac{PA}{ED}$=$\frac{AB}{DB}$，
∴$\frac{x}{DE}$=$\frac{3}{5}$，
∴DE=$\frac{5}{3}$x，
∵点E在射线AD上，点P不与A重合，
∴0＜$\frac{5}{3}$x≤4，
∴0＜x≤$\frac{12}{5}$．

（2）如图②中，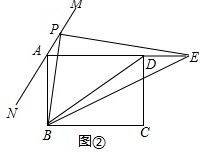

由（1）可知∠BPE=90°，
∵∠BAD=∠BPE，∠ABD=∠PBE，
∴△ABD∽△PBE，
∴$\frac{AB}{PB}$=$\frac{AD}{EP}$，
∴$\frac{PB}{EP}$=$\frac{AB}{AD}$=$\frac{3}{4}$．

（3）①如图①中，

当FA=FP时，∠FAP=∠FPA，
∵△PBE∽ABD，
∴∠PAB=∠FEB，∵∠AFP=∠BFE，
∴∠APF=∠FBE，
∴∠ABE=∠ADB，∵∠BAE=∠BAD，
∴△ABE∽△ADB，
∴BA²=AE•AD，
∴AE=$\frac{9}{4}$，DE=4-$\frac{9}{4}$=$\frac{7}{4}$，
∵DE=$\frac{5}{3}$x，
∴$\frac{5}{3}$x=$\frac{7}{4}$，
∴x=$\frac{21}{20}$，
∴PA=$\frac{21}{20}$．
②如图③中，当AP=AF时，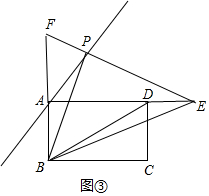

∵∠F=∠F，
∠FPB=∠FAC，
∴△FPB∽△FAC，
∴$\frac{FP}{AF}$=$\frac{FB}{EF}$，
∴$\frac{FP}{FB}$=$\frac{AF}{EF}$，∵∠F=∠F，
∴△FAP∽△FEB，
∴∠FPA=∠FBE，
∵∠F=∠APF，
∴∠F=∠ABE，
∴EF=EB，∵AE⊥BF，
∴AF=AB=AP=3，
综上所述，当AP的值为$\frac{21}{20}$或3时，△PAF是等腰三角形．

点评 本题考查四边形综合题、矩形的性质、相似三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造相似三角形解决问题，属于中考压轴题．