
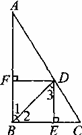
如图所示,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC于E,DF⊥AB于F.
求证:四边形BEDF是正方形.
|
证法一:因为DE⊥BC于E,DF⊥AB于F,∠ABC=90°, 所以∠DFB=∠ABC=∠DEB=90°, 所以四边形BEDF是矩形. 因为BD是∠ABC的平分线,DE⊥BC于E,DF⊥AB于F, 所以DE=DF, 所以矩形BEDF是正方形(有一组邻边相等的矩形是正方形). 证法二:先根据“一组邻边相等的平行四边形是菱形”证四边形BEDF是菱形,再由∠ABC=90°,得菱形BEDF是正方形. 分析:由题设可得∠FBE=90°,∠BED=90°,∠DFB=90°,所以四边形BEDF是矩形.再通过有一组邻边相等的矩形是正方形来证得结论或先证是菱形再证是正方形.由于此题条件更适合先证四边形BEDF是矩形,所以利用有一组邻边相等的矩形是正方形来证更简便一些. |


科目:初中数学 来源: 题型:
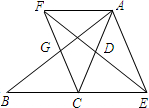 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=查看答案和解析>>
科目:初中数学 来源: 题型:
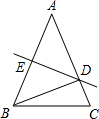 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为查看答案和解析>>
科目:初中数学 来源: 题型:
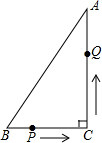 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com