
【题目】如图,平行四边形![]() 中,对角线交于点
中,对角线交于点![]() ,双曲线
,双曲线![]()
![]() 经过
经过![]() 、
、![]() 两点,若平行四边形
两点,若平行四边形![]() 的面积为
的面积为![]() ,则
,则![]() ( )
( )
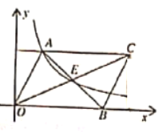
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过A作AD⊥OB于D,过E作EF⊥OB于F,如图,设A(x,![]() ),B(a,0),根据平行四边形的性质得AE=BE,则可判断EF为△BAD的中位线,于是得到EF=
),B(a,0),根据平行四边形的性质得AE=BE,则可判断EF为△BAD的中位线,于是得到EF=![]() AD=
AD=![]() ,DF=
,DF=![]() (a-x),OF=OD+DF=
(a-x),OF=OD+DF=![]() ,则可表示出E(
,则可表示出E(![]() ,
,![]() ),然后根据反比例函数图象上点的坐标特征得到
),然后根据反比例函数图象上点的坐标特征得到![]()
![]() =k,解得a=3x,然后利用平行四边形的面积公式得到关于k的方程,再解方程即可.
=k,解得a=3x,然后利用平行四边形的面积公式得到关于k的方程,再解方程即可.
过A作AD⊥OB于D,过E作EF⊥OB于F,如图,
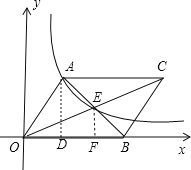
设A(x,![]() ),B(a,0),
),B(a,0),
∵四边形AOBC为平行四边形,
∴AE=BE,
∴EF为△BAD的中位线,
∴EF=![]() AD=
AD=![]() ,
,
∴DF=![]() (a-x),
(a-x),
OF=OD+DF=![]() ,
,
∴ E(![]() ,
,![]() ),
),
∵E点在双曲线上,
∴![]()
![]() =k,
=k,
∴a=3x,
∵平行四边形的面积是12,
∴ADOB=12,
即![]() ,
,
∴![]() ,
,
∴k=4.
故选:B.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个矩形纸片OABC放置在平面直角坐标系xOy内,点A(6,0),点C(0,4),点O(0,0).点P是线段BC上的动点,将△OCP沿OP翻折得到△OC′P.

(Ⅰ)如图①,当点C′落在线段AP上时,求点P的坐标;
(Ⅱ)如图②,当点P为线段BC中点时,求线段BC′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】朝天门,既是重庆城的起源地,也是“未来之城”来福士广场的停泊之地,广场上八幢塔楼临水北向、错落有致,宛如轮扬帆起航,成为我市新的地标性建筑—“朝大杨帆”、来福士广场![]() 塔楼核芯筒于
塔楼核芯筒于![]() 年
年![]() 月
月![]() 日完成结构封顶,高度刷新了重庆的天际线,小明为了测量
日完成结构封顶,高度刷新了重庆的天际线,小明为了测量![]() 的高度,他从塔楼底部
的高度,他从塔楼底部![]() 出发,沿广场前进
出发,沿广场前进![]() 米至点
米至点![]() ,继而沿坡度为
,继而沿坡度为![]() 的斜坡向下走
的斜坡向下走![]() 米到达码头
米到达码头![]() ,然后在浮桥上继续前行
,然后在浮桥上继续前行![]() 米至巡船
米至巡船![]() ,在
,在![]() 处小明操作无人勘测机,当无人勘测机飞行至点
处小明操作无人勘测机,当无人勘测机飞行至点![]() 的正上方点
的正上方点![]() 时,测得码头
时,测得码头![]() 的俯角为
的俯角为![]() 、楼顶
、楼顶![]() 的仰角为
的仰角为![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内,则
在同一平面内,则![]() 塔楼
塔楼![]() 的高度约为多少?(结果精确到
的高度约为多少?(结果精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
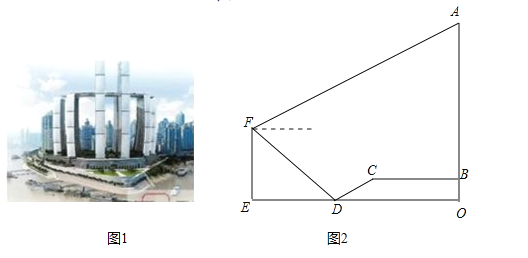
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量大楼![]() 的高度,从距离大楼底部
的高度,从距离大楼底部![]() 30米处的
30米处的![]() ,有一条陡坡公路,车辆从
,有一条陡坡公路,车辆从![]() 沿坡度
沿坡度![]() ,坡面长13米的斜坡到达
,坡面长13米的斜坡到达![]() 后,观测到大楼的顶端
后,观测到大楼的顶端![]() 的仰角为30°,则大楼的高度为( )米.
的仰角为30°,则大楼的高度为( )米.
(精确到0.1米,![]() ,
,![]() )
)
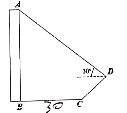
A.26.0B.29.2C.31.1D.32.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市高新区某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的售价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:![]() .
.
(1)工人甲第几天生产的产品数量为60件?
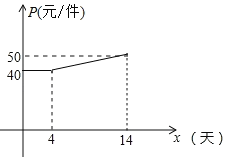
(2)设第x天生产的产品成本为P元/件,P与x的函数关系图象如图,工人甲第x天创造的利润为W元,求W与x的函数关系式,第几天时,利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com