
【题目】如图,已知![]() 、
、![]() 、
、![]() 都与
都与![]() 垂直,垂足分别是
垂直,垂足分别是![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,那么
,那么![]() 的长( )
的长( )
A.6B.9C.12D.16
【答案】C
【解析】
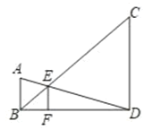
因为AB、CD、EF都与BD垂直,得AB∥CD∥EF,得∠C=∠ABE,∠CDE=∠A,即△ABE∽△DCE,所以![]() ,AB=4,求得BE×CD=4EC,因为EF∥CD,所以∠BEF=∠BCD,∠EBF=∠CBD,∠BFE=∠BDC,即△BEF∽△BCD,即
,AB=4,求得BE×CD=4EC,因为EF∥CD,所以∠BEF=∠BCD,∠EBF=∠CBD,∠BFE=∠BDC,即△BEF∽△BCD,即![]() ,EF=3, 可得BE×CD=3BC=3(BE+EC),即4EC=3BE+3EC,BC=4BE,可求CD;
,EF=3, 可得BE×CD=3BC=3(BE+EC),即4EC=3BE+3EC,BC=4BE,可求CD;
∵AB、CD、EF都与BD垂直,
∴AB∥CD∥EF,
∵AB∥CD,
∴∠C=∠ABE,∠CDE=∠A,
∴△ABE∽△DCE,
∴![]() ,AB=4,
,AB=4,
∴BE×CD=4EC,
∵EF∥CD,
∴∠BEF=∠BCD,∠EBF=∠CBD,∠BFE=∠BDC,
∴△BEF∽△BCD,
∴![]() ,EF=3,
,EF=3,
∴BE×CD=3BC=3(BE+EC),
∴4EC=3BE+3EC,
∴EC=3BE,
∴BC=4BE,
∴![]() =3CD,
=3CD,
∴CD=12;
故选:C.


科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
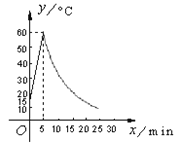
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)

请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10.

(1)尺规作图:作出将△PAC绕点A逆时针旋转60°后所得到的△P′AB(不要求写作法,但需保留作图痕迹).
(2)求点P与点P′之间的距离及∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为了了解九年级学生身体素质情况,从中随机抽取了部分学生进行测试,测试成绩的最高分为30分,最低分为23分,按成绩由低到高分成五组(每组教据可含最大值,不含最小值),绘制的频率分布直方图中缺少了28.5分~30分的一组(如图所示),已知27分~28.5分一组的频率为0.31,且这组学生人数比25.5分~27分这组学生多了28人,根据图示及上述相关信息解答下列问题:
(1)写出从左至右前三组的频率;
(2)在图中补画28.5分~30分一组的小矩形;
(3)求测试时抽样的人数;
(4)求测试成绩的中位数落在第几组;
(5)如果全区共有3600名九年级学生,估计成绩大于27分的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.

(1)如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .
.
①求![]() ,
,![]() 的值;
的值;
②直接写出当![]() 时
时![]() 的范围;
的范围;
(2)如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
①若![]() ,直线
,直线![]() 与函数
与函数![]() 的图象相交点
的图象相交点![]() .当点
.当点![]() 、
、![]() 、
、![]() 中的一点到另外两点的距离相等时,求
中的一点到另外两点的距离相等时,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的平行线与函数
轴的平行线与函数![]() 的图象相交于点
的图象相交于点![]() .当
.当![]() 的值取不大于1的任意实数时,点
的值取不大于1的任意实数时,点![]() 、
、![]() 间的距离与点
间的距离与点![]() 、
、![]() 间的距离之和
间的距离之和![]() 始终是一个定值.求此时
始终是一个定值.求此时![]() 的值及定值
的值及定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
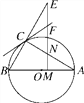
【题目】(如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为2,且AC=CE,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
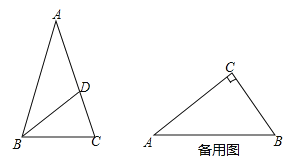
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】玛丽和冯刚做一种游戏,在一个不透明的布袋里装有4个大小、质地均相同小球,球上分别标有数字1、2、3、4,随机从布袋中摸出一个小球,记下数字后放回布袋里,再随机从布袋中摸出一个小球,若这两个小球上的数字之和能被2整除的概率大则玛丽赢;若两个小球上的数字之和能被3整除的概率大则冯刚赢。这个游戏双方公平吗?请列表格或画树状图说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com