
【题目】根据所给信息,回答下列问题.
买![]() 一共要170元,
一共要170元,
买![]() 一共要110元.
一共要110元.
(1)分别求出桌子和椅子的单价是多少?
(2)学校根据实际情况,要求购买桌椅总费用不超过1000元,且购买桌子的数量是椅子数量的![]() ,求该校本次购买桌子和椅子共有哪几种方案?
,求该校本次购买桌子和椅子共有哪几种方案?
【答案】(1)每张椅子20元,每张桌子50元;(2)学校购买桌椅共3种方案.第一种方案:购买6张椅子、15张桌子;第二种方案:购买4张椅子、10张桌子;第三种方案:购买2张椅子、5张桌子.
【解析】
(1)设每张椅子x元,每张桌子y元.由桌子和椅子的单价与总价的关系建立二元一次方程组求出其解即可;(2)设学校购买a张椅子,则桌子的数量为![]() a张.根据购买桌椅总费用不超过1000元列出不等式,解不等式即可求解.
a张.根据购买桌椅总费用不超过1000元列出不等式,解不等式即可求解.
解:(1)设每张椅子x元,每张桌子y元,
根据题意得:![]() ,
,
解得:![]() .
.
答:每张椅子20元,每张桌子50元.
(2)设学校购买a张椅子,则桌子的数量为![]() a张,
a张,
根据题意得:20a+50×![]() a≤1000,
a≤1000,
解得:a≤![]() .
.
∵a、![]() a均为正整数.
a均为正整数.
∴a=6或4或2,
∴学校购买桌椅共3种方案.第一种方案:购买6张椅子、15张桌子;第二种方案:购买4张椅子、10张桌子;第三种方案:购买2张椅子、5张桌子.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,把△ABC先向上平移3个单位长度,再向右平移2个单位长度,得到△A1B1C1.

(1)在图中画出△A1B1C1,并写出点A1、B1、C1的坐标;
(2)连接A1A、C1C,则四边形A1ACC1的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,观察下列图形并解答有关问题:
 ……
……
n=1 n=2 n=3
(1)在第n个图中,共有 块白色瓷砖,共有 块黑色瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中的n的函数关系式(不要求写出自变量的取值范围);
(3)若铺设这样的矩形地面共用了506块瓷砖,通过计算求此时n的值;
(4)是否存在n,使得黑瓷砖与白瓷砖块数相等?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
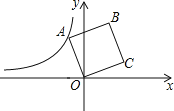
【题目】如图,在平面直角坐标系中,正方形OBCD的顶点O在坐标原点,点B的坐标为(2,5),点A在第二象限,反比例函数 的图象经过点A,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,∠1+∠2=180°,∠A=∠C,试说明:AE∥BC.
解:因为∠1+∠2=180°,
所以AB∥ (同旁内角互补,两直线平行)
所以∠A=∠EDC( ),
又因为∠A=∠C(已知)
所以∠EDC=∠C(等量代换),
所以AE∥BC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:

(1)A,B两城相距多少千米?
(2)分别求甲、乙两车离开A城的距离y与x的关系式.
(3)求乙车出发后几小时追上甲车?
(4)求甲车出发几小时的时候,甲、乙两车相距50千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]()
(1)在平面直角坐标系内画出该函数的图象;
(2)当自变量x=-4时,函数y的值_________;
(3)当x<0时,请结合图象,直接写出y的取值范围:_______.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com