
分析 (1)只要证明当m≠-3时,判别式总大于0即可;
(2)利用一元二次方程根与系数的关系求得两根的积和两根的和,代入即可得到关于m的方程,即可求得m的值.
解答 (1)证明:△=[-3(m-1)]2-4(2m2-6m)
=m2+6m+9
=(m+3)2,
∵m≠-3,
∴(m+3)2>0,
∴当m≠-3时,方程总有两个不相等的实数根;
(2)解:∵x1+x2=3(m-1),x1x2=2m2-6m,两根之积比两根之和大3,
∴2m2-6m-3(m-1)=3,
∴m1=0,m2=$\frac{9}{2}$.
点评 此题主要考查了一元二次方程的判别式与根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 20% | B. | -$\frac{16}{5}$ | C. | 10% | D. | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
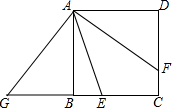 如图,在正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于点F,反向延长BC至G,使BG=DF,连接AG,求证:
如图,在正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于点F,反向延长BC至G,使BG=DF,连接AG,求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com