

分析 (1)设抛物线的解析式为y=a(x+2)(x-8),将点C的坐标代入可求得a的值,从而得到抛物线的解析式,然后依据抛物线的对称性得到抛物线的对称轴方程,将x=3代入可求得抛物线的顶点坐标;
(2)①如图1所示:作CM⊥PE,垂足为M.先利用待定系数法求得BC的解析式,设点P(m,-$\frac{1}{4}$m2+$\frac{3}{2}$m+4),则点E(m,-$\frac{1}{2}$m+4),M(m,4),接下来依据等腰三角形的性质可得到PM=EM,从而得到关于m的方程,于是可求得点P的坐标②作PN⊥BC,垂足为N.先证明△PNE∽△COB,由相似三角形的性质可知PN=$\frac{2\sqrt{5}}{5}$PE,然后再证明△PFN∽△CAF,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得$\frac{PF}{AF}$的最大值;
(3)设⊙Q与直线CD的切点为G,连接QG,过点C作CH⊥QD于H,如图3所示:先依据勾股定理可求得DC的长,设Q(3,b),然后依据锐角三角函数的定义得到QG的长,从而得到AQ的长,最后再△AQP中依据勾股定理可得到关于b的方程,从而得到点Q的坐标.
解答 解:(1)设抛物线的解析式为y=a(x+2)(x-8).
∵抛物线经过点C(0,4),
∴-16a=4,解得a=-$\frac{1}{4}$.
∴抛物线的解析式为y=-$\frac{1}{4}$(x+2)(x-8)=$-\frac{1}{4}$x2+$\frac{3}{2}$x+4.
∵A(-2,0)、B(8,0),
∴抛物线的对称轴为x=3.
∵将x=3代入得:y=$\frac{25}{4}$,
∴抛物线的顶点坐标为(3,$\frac{25}{4}$).
(2)①如图1所示:作CM⊥PE,垂足为M.
设直线BC的解析式为y=kx+b.
∵将B、C的坐标代入得:$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$,解得k=-$\frac{1}{2}$,b=4,
∴直线BC的解析式为y=-$\frac{1}{2}$x+4.
设点P(m,-$\frac{1}{4}$m2+$\frac{3}{2}$m+4),则点E(m,-$\frac{1}{2}$m+4),M(m,4).
∵PC=EC,CM⊥PE,
∴PM=EM.
∴-$\frac{1}{4}$m2+$\frac{3}{2}$m+4-4=4-(-$\frac{1}{2}$m+4),解得:m=0(舍去),m=4.
∴P(4,6).
②作PN⊥BC,垂足为N.
由①得:PE=-$\frac{1}{4}$m2+2m.
∵PE∥y轴,PN⊥BC,
∴∠PNE=∠COB=90°,∠PEN=∠BCO.
∴△PNE∽△BOC.
∴$\frac{PN}{PE}=\frac{OB}{BC}$=$\frac{8}{4\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
∴PN=$\frac{2\sqrt{5}}{5}$PE=$\frac{2\sqrt{5}}{5}$(-$\frac{1}{4}$m2+2m).
∵AB=10,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,
∴AC2+BC2=AB2.
∴∠BCA=90°,
又∵∠PFN=∠CFA,
∴△PFN∽△CAF.
∴$\frac{PF}{AF}=\frac{PN}{AC}$=$\frac{\frac{2\sqrt{5}}{5}(-\frac{1}{4}{m}^{2}+2m)}{2\sqrt{5}}$=-$\frac{1}{20}$m2+$\frac{2}{5}$m.
∴当m=4时,$\frac{PF}{AF}$的最大值为$\frac{4}{5}$.
(3)设⊙Q与直线CD的切点为G,连接QG,过点C作CH⊥QD于H,如图3所示:
由(1)可知:CH=3,DH=$\frac{25}{4}$-4=$\frac{9}{4}$.
在△CHD中,由勾股定理可知DC=$\sqrt{{3}^{2}+(\frac{9}{4})^{2}}$=$\frac{15}{4}$.
设Q(3,b)则QD=$\frac{25}{4}$-b.
∵sin∠D=$\frac{CH}{DC}=\frac{QG}{DQ}$=$\frac{4}{5}$,
在△AQP中,由勾股定理得QG=$\frac{4}{5}$($\frac{25}{4}$-b)=b2+52.
解得:b=0,b=-$\frac{200}{9}$.
∴点Q的坐标为(3,0)或(3,-$\frac{200}{9}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、一次函数的解析式、等腰三角形的性质、锐角三角函数的定义、勾股定理的应用,$\frac{PF}{AF}$与m的函数关系式是解题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
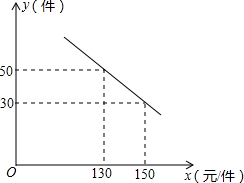 某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com