
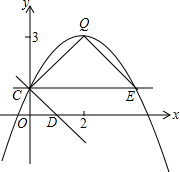
 ��ͼ��������y=ax2+bx+c��a��0����ͼ�����C��0��1��������ΪQ��2��3������D��x���������ϣ���OD=OC
��ͼ��������y=ax2+bx+c��a��0����ͼ�����C��0��1��������ΪQ��2��3������D��x���������ϣ���OD=OC���� ��1�����ô���ϵ������������ߵĽ���ʽ��
��2������֤����CEQ���CDO��Ϊ����ֱ�������Σ������ó���CEQ�ס�CDO��
��3�������ͼ����ʾ������C����ֱ��QE�ĶԳƵ�C�䣬����C����x��ĶԳƵ�C�壬����C��C�壬��OD�ڵ�F����QE�ڵ�P�����PCF��Ϊ����������ܳ���С�������Σ�����ԳƵ����ʿ�֪����PCF���ܳ������߶�C��C��ij��ȣ�������ԳƵ����ʡ�����֮���߶���̿���֤����ʱ��PCF���ܳ���С��
���ͼ����ʾ�����ù��ɶ�������߶�C��C��ij��ȣ�����PCF�ܳ�����Сֵ��
�����ö��κ���ƽ�Ƶ���������Ҽ��Լ���ϵ������ó���QCE�Ķ�������������ɣ�
��� �⣺��1���������ߵĽ���ʽΪy=a��x-2��2+3��
��C��0��1������ã�1=a����-2��2+3��
���a=-$\frac{1}{2}$��
��y=-$\frac{1}{2}$��x-2��2+3=-$\frac{1}{2}$x2+2x+1��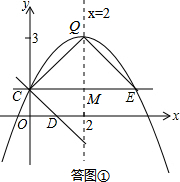
��2��֤�����������֪����ECD=45�㣬
��OC=OD����OC��OD��
���OCDΪ����ֱ�������Σ���ODC=45�㣬
���ECD=��ODC��
��CE��x�ᣬ���C��E���ڶԳ��ᣨֱ��x=2���Գƣ�
���E��������4��1����
���ͼ����ʾ����Գ��ᣨֱ��x=2����CE���ڵ�M����M��2��1����
��ME=CM=QM=2��
���QME���QMC��Ϊ����ֱ�������Σ�
���QEC=��QCE=45�㣮
�֡ߡ�OCDΪ����ֱ�������Σ�
���ODC=��OCD=45�㣬
���QEC=��QCE=��ODC=��OCD=45�㣬
���CEQ�ס�CDO��
��3���ٴ��ڣ�
���ͼ����ʾ������C����ֱ��QE�ĶԳƵ�C�䣬����C����x��ĶԳƵ�C�壬����C��C�壬��OD�ڵ�F����QE�ڵ�P�����PCF��Ϊ����������ܳ���С�������Σ�����ԳƵ����ʿ�֪����PCF���ܳ������߶�C��C��ij��ȣ�
��֤�����£��������߶�OD��ȡ���ڵ�F����һ��F�䣬���߶�QE��ȡ���ڵ�P����һ��P�䣬����F��C�壬F��P�䣬P��C�䣮
����ԳƵ����ʿ�֪����P��CF����ܳ�=F��C��+F��P��+P��C�䣻
��F��C��+F��P��+P��C���ǵ�C�䣬C��֮������߶Σ�
������֮���߶���̿�֪��F��C��+F��P��+P��C�䣾C��C�壬
����P��CF����ܳ����ڡ�PCE���ܳ�����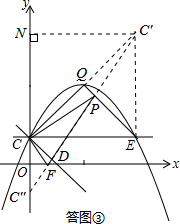
���ͼ����ʾ������C��E��
��C��C�����ֱ��QE�Գƣ���QCEΪ����ֱ�������Σ�
���QC��EΪ����ֱ�������Σ�
���CEC��Ϊ����ֱ�������Σ�
���C���������4��5����
��C��C�����x��Գƣ����C�������Ϊ��0��-1����
����C����C��N��y���ڵ�N����NC��=4��NC��=4+1+1=6��
��Rt��C��NC���У��ɹ��ɶ����ã�C��C��=$\sqrt{C��{N}^{2}+C��{N}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$��
������������P���F���ƶ������У���PCF���ܳ�������Сֵ����СֵΪ2$\sqrt{13}$��
�ڡ�C��0��1����Q��2��3����
��ɵá�QCE=45�㣬����������QC����ƽ��$\sqrt{2}$����λ��������ߵĽ���ʽ�൱������ƽ��1����λ��
������ƽ��1����λ�õ��ĺ�������ʽ����ƽ�ƺ����ʽΪ��y=-$\frac{1}{2}$��x-1��2+2��
���� ���⿼���˶��κ�����ͼ�������ʡ�����ϵ���������������Ρ�����ֱ�������Ρ����ɶ�������ԳƵ����ʵ���Ҫ֪ʶ�㣬�漰����϶࣬��һ����Ѷȣ������ѵ����ڵڣ�3���ʣ���γ��������ԳƵ�����ȷ����PCF�ܳ���Сʱ�ļ���ͼ�Σ��ǽ����Ĺؼ���


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
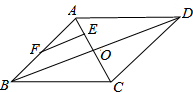 ��ͼ������ABCD�ı߳�Ϊ4����ABC=60�㣬��E��F�ֱ�ΪAO��AB���е㣬��EF�ij���Ϊ��������
��ͼ������ABCD�ı߳�Ϊ4����ABC=60�㣬��E��F�ֱ�ΪAO��AB���е㣬��EF�ij���Ϊ��������| A�� | 4 | B�� | 3 | C�� | 2$\sqrt{3}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
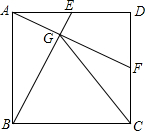 ��ͼ����������ABCD�У�E��F�ֱ���AD��DC���е㣬AF��BE���ڵ�G������CG����˵������CGB�ǵ��������Σ�
��ͼ����������ABCD�У�E��F�ֱ���AD��DC���е㣬AF��BE���ڵ�G������CG����˵������CGB�ǵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
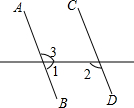 ��ͼ����֪��1=70�㣬ҪʹAB��CD������߱�����һ�������ǣ�������
��ͼ����֪��1=70�㣬ҪʹAB��CD������߱�����һ�������ǣ�������| A�� | ��2=70�� | B�� | ��2=100�� | C�� | ��2=110�� | D�� | ��3=110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com