
【题目】如图,已知平行四边形![]() 对角线
对角线![]() 与
与![]() 交于点
交于点![]() 以
以![]() 边分别为边长作正方形
边分别为边长作正方形![]() 正方形
正方形![]() ,连接
,连接![]() .
.
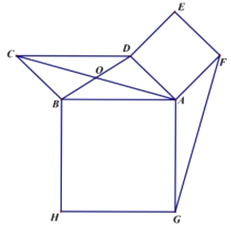
(1)求证:![]() ;
;
(2)若![]() ,请求出
,请求出![]() 的面积.
的面积.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
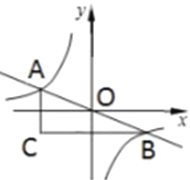
【题目】如图,在平面直角坐标系中,过原点的直线与反比例函数![]() 交于点
交于点![]() ,与反比例函数
,与反比例函数 ![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,过点
轴的垂线,过点![]() 作
作![]() 轴的垂线,两直线交于点
轴的垂线,两直线交于点![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对博鳌论坛会的了解情况,某中学随机抽取了部分学生进行问卷调查,将调查结果记作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解较少,
了解较少,![]() 不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
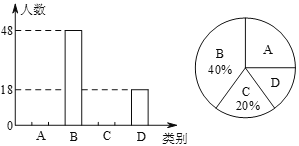
(1)此次共调查了______名学生;扇形统计图中![]() 所在的扇形的圆心角度数为______;
所在的扇形的圆心角度数为______;
(2)将条形统计图补充完整;
(3)若该校共有1600名学生,请你估计对博鳌论坛会的了解情况为“非常了解”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
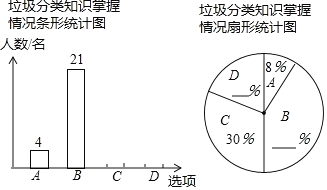
【题目】为响应市政府关于“垃圾不落地市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生有2000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有 名;
(3)已知“非常了解”的同学有3名男生和1名女生,从中随机抽取2名进行垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
| ··· |
|
|
|
| ··· |
| ··· |
|
|
|
| ··· |
下列结论错误的是( )
A.![]() B.
B.![]() 是关于
是关于![]() 的方程
的方程![]() 的一个根;
的一个根;
C.当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;D.当
值的增大而减小;D.当![]() 时,
时,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点
,顶点![]() 的横坐标为
的横坐标为![]() ,对称轴交
,对称轴交![]() 轴交于点
轴交于点![]() ,交
,交![]() 与点
与点![]() .
.
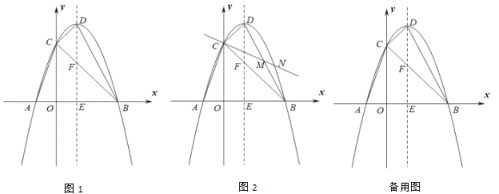
(1)求顶点![]() 的坐标;
的坐标;
(2)如图2所示,过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
①若直线![]() 将
将![]() 分成的两部分面积之比为
分成的两部分面积之比为![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
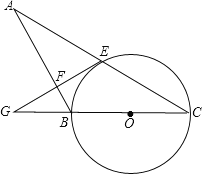
【题目】如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若GF=2![]() ,GB=4,求⊙O的半径.
,GB=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com