
【题目】某商店经过市场调查,整理出某种商品在第![]() (
(![]() )天的售价与销量的相关信息如下表.已知该商品的进价为每件30元,设销售该商品每天的利润为
)天的售价与销量的相关信息如下表.已知该商品的进价为每件30元,设销售该商品每天的利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系是;
的函数关系是;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
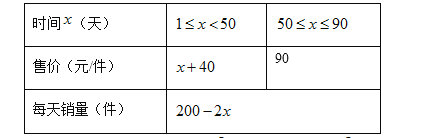
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
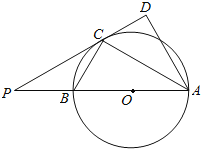
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB.延长DC交AB的延长线于点P.
(1)求证:PC2=PAPB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?

查看答案和解析>>
科目:初中数学 来源: 题型:
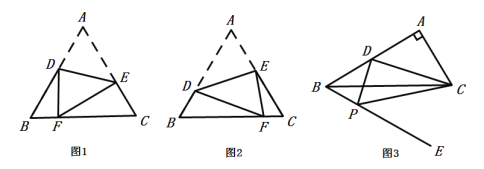
【题目】(1)如图1,△ABC为等边三角形,点D、E分别为边AB、AC上的一点,将图形沿线段DE所在的直线翻折,使点A落在BC边上的点F处求证:![]() ;
;
(2)如图2,按图1的翻折方式,若等边△ABC的边长为4,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图3,在![]() 中,
中,![]() ,点D是AB边上的中点,在BC的下方作射线BE,使得
,点D是AB边上的中点,在BC的下方作射线BE,使得![]() ,点P是射线BE上一个动点,当
,点P是射线BE上一个动点,当![]() ,求BP的长.
,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
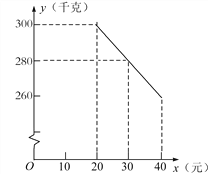
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC,BC分別与⊙O交于点D,E,则下列说法一定正确的是( )
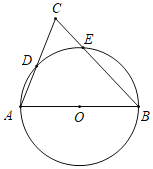
A.连接BD,可知BD是△ABC的中线B.连接AE,可知AE是△ABC的高线
C.连接DE,可知![]() D.连接DE,可知S△CDE:S△ABC=DE:AB
D.连接DE,可知S△CDE:S△ABC=DE:AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com