练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知⊙0的半径为4cm，点O到直线a的距离为4cm，则⊙O与直线a的位置关系是相切．

    分析 已知圆的半径为r，圆心到直线的距离为d，当d＞r时，直线与圆相离，当d=r时，直线与圆相切，当d＜r时，直线与圆相交，根据以上内容判断即可．

    解答 解：∵⊙0的半径为4cm，点O到直线a的距离为4cm，
    4=4，
    ∴⊙O与直线a的位置关系是相切，
    故答案为：相切．

    点评 本题考查了直线和圆的位置关系的应用，能熟记直线和圆的位置关系的内容是解此题的关键，注意：直线和圆有三种位置关系：相离，相交，相切，已知：圆的半径为r，圆心到直线的距离为d，当d＞r时，直线与圆相离，当d=r时，直线与圆相切，当d＜r时，直线与圆相交．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．如图，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBQ重合，若PB=3，求PQ的长为3$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．小明家想利用房屋侧面的一面墙，再砌三面墙，围成一个矩形猪圈，如图所示，一面墙的中间留出1米宽的进出门（门使用另外的材料）．现备有足够砌15米长的围墙的材料，设猪圈与已有墙面垂直的墙的长度为x米．
    （1）要使猪圈面积为24平方米，如何设计三面围墙的长度．
    （3）能否使猪圈面积为36平方米？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．若数据5-a，5，5+a的方差为6，则a=±3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知二次函数y=x2-2，当-1≤x≤2时，y的取值范围是-1≤y≤2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．已知四个三角形的三个内角的比分别是1：3：4，2：5：7，1：3：5，2：6：9，在这四个三角形中，直角三角形有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

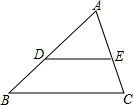    6．如图，在△ABC中，D、E分别在AB、AC上，且$\frac{AD}{AB}$=$\frac{AE}{AC}$，如果AE=3.6cm，EC=2.4cm，AB=9cm．求AD和BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

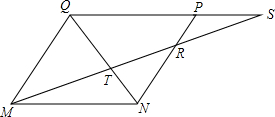    3．如图，已知MNPQ为平行四边形，在QP的延长线上任取-点S，直线MS与NQ交于点T，与NP交于点R．求证：$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．点C在线段AB上，AC=8cm，CB=6cm，点M，N分别是AC，BC的中点．
    （1）求线段MN的长．
    （2）若C为线段AB上任一点，满足AC+CB=acm，其他条件不变，你能猜想MN的长度吗？并说明理由．
    （3）若C在线段AB的延长线上，且满足AC-CB=bcm，M，N分别为AC，BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由．
    拓展附加题：阅读下列材料并填空：
    （1）探究：平面上有n个点（n≥2）且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？
    我们知道，两点确定一条直线．平面上有2个点时，可以画$\frac{2×1}{2}$=1条直线，平面内有3个点时，一共可以画$\frac{3×2}{2}$=3条直线，平面上有4个点时，一共可以画$\frac{4×3}{2}$=6条直线，平面内有5个点时，一共可以画10条直线，平面内有n个点时，一共可以画多少条直线？
    （2）迁移：某足球联赛实行单循环比赛（每两队之间必须比赛一场），有2支球队时，要进行$\frac{2×1}{2}$=1场比赛，有3个球队时，要进行$\frac{3×2}{2}$=3场比赛，有4个球队时，要进行6场比赛，那么有20个球队时，要进行多少场比赛？

    查看答案和解析>>

    同步练习册答案