Question

如图，直线y＝hx＋d与x轴和y轴分别相交于点A(－1，0)，B(0，1)，与双曲线y＝在第一象限相交于点C；以AC为斜边、∠CAO为内角的直角三角形，与以CO为对角线、一边在x轴上的矩形面积相等；点C，P在以B为顶点的抛物线y＝mx²＋nx＋k上；直线y＝hx＋d、双曲线y＝和抛物线y＝ax²＋bx＋c同时经过两个不同的点C，D．

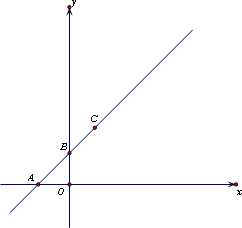
(1)确定t的值

(2)确定m，n，k的值

(3)若无论a，b，c取何值，抛物线y＝ax²＋bx＋c都不经过点P，请确定P的坐标

Answer 1

答案：
解析：

解：(1)直线过点A，B，则0＝－h＋d和1＝d，即y＝x＋1．1分 　　双曲线y＝经过点C(x1，y1)，x1y1＝t． 　　以AC为斜边，∠CAO为内角的直角三角形的面积为×y1×(1＋x1)； 　　以CO为对角线的矩形面积为7x1y1， 　　×y1×(1＋x1)＝x1y1，因为x1，y1都不等于0，故得x1＝1，所以y1＝2. 　　故有，，即t＝2．2分 　　(2)∵B是抛物线y＝mx2＋nx＋k的顶点，∴有－， 　　得到n＝0，k＝1．3分 　　∵C是抛物线y＝mx2＋nx＋k上的点，∴有2＝m(1)2＋1，得m＝1．4分 　　(3)设点P的横坐标为p，则纵坐标为p2＋1. 　　∵抛物线y＝ax2＋bx＋c经过两个不同的点C，D7， 　　其中求得D点坐标为(－2，－1)．5分. 　　解法一： 　　故2＝a＋b＋c， 　　－1＝4a－2b＋c． 　　解之得，b＝a＋1，c＝1－2A．6分 　　(说明：如用b表示a，c，或用c表示a，b，均可，后续参照得分) 　　∴y＝ax2＋(a＋1)x＋(1－2a) 　　于是：p2＋1≠a，p2＋(a＋1)p＋(1－2a)　　7分 　　∴无论a取什么值都有p2－p≠(p2＋p－2)a．8分 　　(或者，令p2－p＝(p2＋p－2)a　　7分 　　∵抛物线y＝ax2＋bx＋c不经过P点， 　　∴此7方程无解，或有解但不合题意8分) 　　故∵a≠0，∴① 　　解之p＝0，p＝1，并且p≠1，p≠－2．得p＝0．9分 　　∴符合题意的P点为(0，1)．　　10分 　　②，解之p＝1，p＝－2，并且p≠0，p≠1． 　　得p＝－2．　　11分 　　符合题意的P点为(－2，5)．　　12分 　　∴符合题意的P点有两个(0，1)和(－2，5)． 　　解法二： 　　则有(a－1)p2＋(a＋1)p－2a＝0　　7分 　　即〔(a－1)p＋2a〕(p－1)＝0 　　有p－1＝0时，得p＝1，为(1，2)此即C点，在y＝ax2＋bx＋c上．8分 　　或(a－1)p＋2a＝0，即(p＋2)a＝p 　　当p＝0时a＝0与a≠0矛盾　　9分 　　得点P(0，1)　　10分 　　或者p＝－2时，无解　　11分 　　得点P(－2，5)　　12分 　　故对任意a，b，c，抛物线y＝ax2＋bx＋c都不经过(0，1)和(－2，5) 　　解法三： 　　如图，抛物线y＝ax2＋bx＋c不经过直线CD上除C，D外的其他点． 　　(只经过直线CD上的C，D点)．　　6分 　　由　　7分 　　解得交点为C(1，2)，B(0，1)． 　　故符合题意的点P为(0，1)．8分 　　抛物线y＝ax2＋bx＋c不经过直线x＝－2上除D外的其他点．9分 　　由　　10分 　　解得交点P为(－2，5)．11分 　　抛物线y＝ax2＋bx＋c不经过直线x＝1上除C外的其他点， 　　而解得交点为C(1，2)．12分 　　故符合条件的点P为(0，1)或(－2，5) 　　(说明：1仅由图形看出一个点的坐标给1分，二个看出来给2分2解题过程叙述基本清楚即可)