
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß y=![]() x2©
x2©![]() x©
x©![]() ÓėxÖį½»ÓŚA”¢B”¢Į½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£®
ÓėxÖį½»ÓŚA”¢B”¢Į½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£®
£Ø1£©ÅŠ¶Ļ”÷ABCŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
£Ø2£©ŌŚÅ×ĪļĻßµŚĖÄĻóĻŽÉĻÓŠŅ»µć£¬Ėü¹ŲÓŚxÖįµÄ¶Ō³Ęµć¼ĒĪŖµćP£¬µćMŹĒÖ±ĻßBCÉĻµÄŅ»¶Æµć£¬µ±”÷PBCµÄĆ껿×ī“óŹ±£¬ĒóPM+![]() MCµÄ×īŠ”Öµ£»
MCµÄ×īŠ”Öµ£»
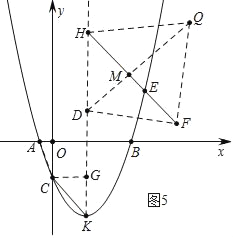
£Ø3£©ČēĶ¼2£¬µćKĪŖÅ×ĪļĻߵĶ„µć£¬µćDŌŚÅ×ĪļĻ߶Ō³ĘÖįÉĻĒŅׯ×ų±źĪŖ![]() £¬¶Ō³ĘÖįÓŅ²ąµÄÅ×ĪļĻßÉĻÓŠŅ»¶ÆµćE£¬¹żµćE×÷EH”ĪCK£¬½»¶Ō³ĘÖįÓŚµćH£¬ŃÓ³¤HEÖĮµćF£¬Ź¹µĆEF=
£¬¶Ō³ĘÖįÓŅ²ąµÄÅ×ĪļĻßÉĻÓŠŅ»¶ÆµćE£¬¹żµćE×÷EH”ĪCK£¬½»¶Ō³ĘÖįÓŚµćH£¬ŃÓ³¤HEÖĮµćF£¬Ź¹µĆEF=![]() £¬ŌŚĘ½ĆęÄŚÕŅŅ»µćQ£¬Ź¹µĆŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±Ļß ŹĒ¶Ō³ĘÖį£¬ĒėĪŹŹĒ·ń“ęŌŚÕāŃłµÄµćQ£¬Čō“ęŌŚĒėÖ±½ÓŠ“³öµćEµÄŗį×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£¬ŌŚĘ½ĆęÄŚÕŅŅ»µćQ£¬Ź¹µĆŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±Ļß ŹĒ¶Ō³ĘÖį£¬ĒėĪŹŹĒ·ń“ęŌŚÕāŃłµÄµćQ£¬Čō“ęŌŚĒėÖ±½ÓŠ“³öµćEµÄŗį×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©½įĀŪ£ŗ”÷ABCŹĒÖ±½ĒČż½ĒŠĪ£Ø2£©![]() £Ø3£©“ęŌŚ£®Āś×ćĢõ¼žµÄµćEµÄŗį×ų±źĪŖ
£Ø3£©“ęŌŚ£®Āś×ćĢõ¼žµÄµćEµÄŗį×ų±źĪŖ![]() »ņ
»ņ![]() »ņ
»ņ![]() »ņ
»ņ![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉ”÷AOC”×”÷COB£¬ĶĘ³ö”ĻACO=”ĻOBC£¬ÓÉ”ĻOBC+”ĻOCB=90”ć£¬ĶĘ³ö”ĻACO+”ĻBCO=90”ć£¬ĶĘ³ö”ĻACB=90”ć£¬µĆ³ö½įĀŪ£»
£Ø2£©ČēĶ¼1ÖŠ£¬É赌ĖÄĻóĻŽÅ×ĪļĻßÉĻŅ»µćN£Øm£¬ ![]() x2©
x2©![]() x©
x©![]() £©£¬µćN¹ŲÓŚxÖįµÄ¶Ō³ĘµćP£Øm£¬-
£©£¬µćN¹ŲÓŚxÖįµÄ¶Ō³ĘµćP£Øm£¬-![]() x2+
x2+![]() x+
x+![]() £©£¬×÷¹żB”¢C·Ö±š×÷yÖį”¢xÖįµÄĘ½ŠŠĻß½»ÓŚµćG£¬Į¬½ÓPG£¬æɵĆS”÷PBC=S”÷PCG+S”÷PBG©S”÷BCG£¬ÓÉ“ĖæɵƔ÷PBCĆ껿×ī“󏱵ĵćPµÄ×ų±ź£¬ČēĶ¼2£¬×÷ME”ĶCGÓŚµćM£¬ÓÉ”÷CEM”×”÷BOC£¬øł¾Ż¶ŌÓ¦±ß³É±ČĄż£¬µĆ³öPM+
£©£¬×÷¹żB”¢C·Ö±š×÷yÖį”¢xÖįµÄĘ½ŠŠĻß½»ÓŚµćG£¬Į¬½ÓPG£¬æɵĆS”÷PBC=S”÷PCG+S”÷PBG©S”÷BCG£¬ÓÉ“ĖæɵƔ÷PBCĆ껿×ī“󏱵ĵćPµÄ×ų±ź£¬ČēĶ¼2£¬×÷ME”ĶCGÓŚµćM£¬ÓÉ”÷CEM”×”÷BOC£¬øł¾Ż¶ŌÓ¦±ß³É±ČĄż£¬µĆ³öPM+![]() CM=PM+ME£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±PE”ĶCGŹ±£¬PM+ME×ī¶Ģ£¬ÓÉ“Ė¼“æɽā¾ö£»
CM=PM+ME£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±PE”ĶCGŹ±£¬PM+ME×ī¶Ģ£¬ÓÉ“Ė¼“æɽā¾ö£»
£Ø3£©·ÖČżÖÖĒéæöĢÖĀŪ£¬¢ŁČēĶ¼3£¬µ±DH=HF£¬HQĘ½·Ö”ĻDHFŹ±£¬ŅŌąĒF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±ĻߏĒ¶Ō³ĘÖį£¬¢ŚČēĶ¼4£¬µ±DH=HF£¬HQĘ½·Ö”ĻDHFŹ±£¬ŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±ĻߏĒ¶Ō³ĘÖį£¬¢ŪČēĶ¼5£¬µ±DH=DF£¬DQĘ½·Ö”ĻHDFŹ±£¬ŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±ĻߏĒ¶Ō³ĘÖį£¬·Ö±šĒó½ā¼“æÉ.
ŹŌĢā½āĪö£ŗ£Ø1£©½įĀŪ£ŗ”÷ABCŹĒÖ±½ĒČż½ĒŠĪ£®ĄķÓÉČēĻĀ£¬
¶ŌÓŚÅ×ĪļĻß y=![]() x2©
x2©![]() x©
x©![]() £¬Įīy=0µĆ
£¬Įīy=0µĆ ![]() x2©
x2©![]() x©
x©![]() =0£¬½āµĆx=©
=0£¬½āµĆx=©![]() »ņ3
»ņ3![]() £»Įīx=0µĆy=©
£»Įīx=0µĆy=©![]() £¬
£¬
”ąA£Ø©![]() £¬0£©£¬C£Ø0£¬©
£¬0£©£¬C£Ø0£¬©![]() £©£¬B£Ø3
£©£¬B£Ø3![]() £¬0£©£¬
£¬0£©£¬
”ąOA=![]() £¬OC=
£¬OC=![]() £¬OB=3
£¬OB=3![]() £¬
£¬
”ą![]() =
=![]() =
=![]() £¬”ß”ĻAOC=”ĻBOC£¬
£¬”ß”ĻAOC=”ĻBOC£¬
”ą”÷AOC”×”÷COB£¬
”ą”ĻACO=”ĻOBC£¬
”ß”ĻOBC+”ĻOCB=90”ć£¬
”ą”ĻACO+”ĻBCO=90”ć£¬
”ą”ĻACB=90”ć£®
£ØŅ²æÉŅŌĒó³öAC”¢BC”¢ABĄūÓĆ¹“¹É¶ØĄķµÄÄę¶ØĄķÖ¤Ć÷£©£®
£Ø2£©ČēĶ¼1ÖŠ£¬É赌ĖÄĻóĻŽÅ×ĪļĻßÉĻŅ»µćN£Øm£¬![]() m2©
m2©![]() m©
m©![]() £©£¬µćN¹ŲÓŚxÖįµÄ¶Ō³ĘµćP£Øm£¬©
£©£¬µćN¹ŲÓŚxÖįµÄ¶Ō³ĘµćP£Øm£¬©![]() m2+
m2+![]() m+
m+![]() £©£¬×÷¹żB”¢C·Ö±š×÷yÖį£¬xÖįµÄĘ½ŠŠĻß½»ÓŚµćG£¬Į¬½ÓPG£®
£©£¬×÷¹żB”¢C·Ö±š×÷yÖį£¬xÖįµÄĘ½ŠŠĻß½»ÓŚµćG£¬Į¬½ÓPG£®
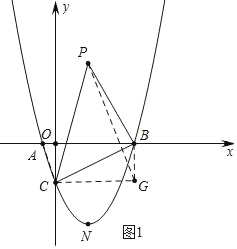
”ßG£Ø3![]() £¬©
£¬©![]() £©£¬
£©£¬
”ąS”÷PBC=S”÷PCG+S”÷PBG©S”÷BCG=![]() ”Į
”Į![]() ”Į£Ø©
”Į£Ø©![]() m2+
m2+![]() m+2
m+2![]() £©+
£©+![]() ”Į
”Į![]() £Ø3
£Ø3![]() ©m£©©
©m£©©![]() ”Į
”Į![]() ”Į
”Į![]() =©
=©![]() £Øm©
£Øm©![]() £©2+
£©2+![]() £®
£®
”ß©![]() £¼0£¬
£¼0£¬
”ąµ±m=![]() Ź±£¬”÷PBCµÄĆ껿×ī“ó£¬
Ź±£¬”÷PBCµÄĆ껿×ī“ó£¬
“ĖŹ±P£Ø![]() £¬
£¬![]() £©£¬
£©£¬
ČēĶ¼2ÖŠ£¬×÷ME”ĶCGÓŚM£®
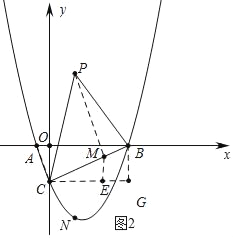
”ßCG”ĪOB£¬
”ą”ĻOBC=”ĻECM£¬”ß”ĻBOC=”ĻCEM£¬
”ą”÷CEM”×”÷BOC£¬
”ßOC£ŗOB£ŗBC=1£ŗ3£ŗ![]() £¬
£¬
”ąEM£ŗCE£ŗCM=1£ŗ3£ŗ![]() £¬
£¬
”ąEM=![]() CM£¬
CM£¬
”ąPM+![]() CM=PM+ME£¬
CM=PM+ME£¬
”ąøł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±PE”ĶCGŹ±£¬PM+ME×ī¶Ģ£¬
”ąPM+![]() MCµÄ×īŠ”ÖµĪŖ
MCµÄ×īŠ”ÖµĪŖ![]() +
+![]() =
=![]() £®
£®
£Ø3£©“ęŌŚ£®ĄķÓÉČēĻĀ£¬
¢ŁČēĶ¼3ÖŠ£¬µ±DH=HF£¬HQĘ½·Ö”ĻDHFŹ±£¬ŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±Ļß ŹĒ¶Ō³ĘÖį£®
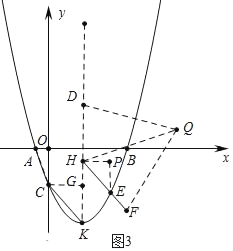
×÷CG”ĶHKÓŚG£¬PH”ĪxÖį£¬EP”ĶPHÓŚP£®
”ßFH”ĪCK£¬K£Ø![]()
![]() £¬©
£¬©![]()
![]() £©£¬
£©£¬
Ņ×ÖŖCG£ŗGK£ŗCK=3£ŗ4£ŗ5£¬
ÓÉ”÷EPH”×”÷KGC£¬µĆPH£ŗPE£ŗEH=3£ŗ4£ŗ5£¬ÉčE£Ø£Øn£¬![]() n2©
n2©![]() n©
n©![]() £©£¬ŌņHE=
£©£¬ŌņHE=![]() £Øn©
£Øn©![]()
![]() £©£¬PE=
£©£¬PE=![]() £Øn©
£Øn©![]()
![]() £©£¬
£©£¬
”ßDH=HF£¬
”ą![]() +[©
+[©![]() n2+
n2+![]() n+
n+![]() ©
©![]() £Øn©
£Øn©![]()
![]() £©]=
£©]=![]() £Øn©
£Øn©![]()
![]() £©+
£©+![]()
![]() £¬
£¬
½āµĆn=![]() »ņ
»ņ![]() £ØÉįĘś£©£®
£ØÉįĘś£©£®
¢ŚČēĶ¼4ÖŠ£¬µ±DH=HF£¬HQĘ½·Ö”ĻDHFŹ±£¬ŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±Ļß ŹĒ¶Ō³ĘÖį£®
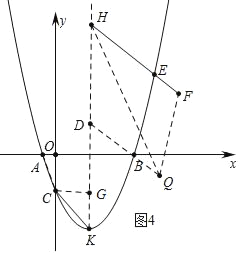
Ķ¬·ØæɵĆ[![]() n2©
n2©![]() n©
n©![]() +
+![]() £Øn©
£Øn©![]()
![]() £©]©
£©]©![]() =
=![]() £Øn©
£Øn©![]()
![]() £©+
£©+![]()
![]() £¬
£¬
½āµĆn=![]() +
+![]() »ņ
»ņ![]() ©
©![]() £ØÉįĘś£©£®
£ØÉįĘś£©£®
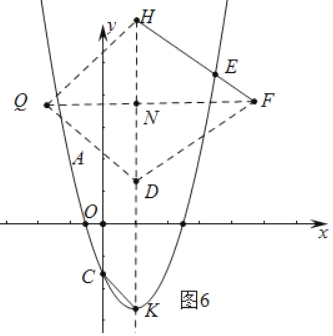
¢ŪČēĶ¼5ÖŠ£¬µ±DH=DF£¬DQĘ½·Ö”ĻHDFŹ±£¬ŅŌµćF”¢H”¢D”¢QĪŖ¶„µćµÄĖıߊĪŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅ¹żµćQµÄ¶Ō½ĒĻßĖłŌŚµÄÖ±Ļß ŹĒ¶Ō³ĘÖį£®
ÉčDQ½»HFÓŚM£®ÓÉ”÷DHM”×”÷CKG£¬æÉÖŖHM£ŗDH=4£ŗ5£¬
![]() [
[![]() £Øn©
£Øn©![]()
![]() £©+
£©+![]()
![]() ]£ŗ[
]£ŗ[![]() n2©
n2©![]() n©
n©![]() +
+![]() £Øn©
£Øn©![]()
![]() £©©
£©©![]() ]=4£ŗ5£¬
]=4£ŗ5£¬
½āµĆn=![]() +
+![]() »ņ=
»ņ=![]() ©
©![]() £ØÉįĘś£©£¬
£ØÉįĘś£©£¬
¢ÜČēĶ¼6ÖŠ£¬µ±FQĘ½·Ö”ĻDFHŹ±£¬Āś×ćĢõ¼ž£¬“ĖŹ±![]() =
=![]() £®
£®
”ą5”Į![]() [
[![]() n2©
n2©![]() n©
n©![]() ©
©![]() +
+![]() £Øn©
£Øn©![]()
![]() £©]=4[
£©]=4[![]() £Øn©
£Øn©![]()
![]() £©+
£©+![]()
![]() ]£¬
]£¬
½āµĆ£ŗn=![]() »ņ
»ņ![]() £ØÉįĘś£©
£ØÉįĘś£©
×ŪÉĻĖł£¬Āś×ćĢõ¼žµÄµćEµÄŗį×ų±źĪŖ![]() »ņ
»ņ![]() +
+![]() »ņ
»ņ![]() +
+![]() »ņ
»ņ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬CŹĒ”ŃOÉĻŅ»µć£¬DŌŚABµÄŃÓ³¤ĻßÉĻ£¬ĒŅ”ĻBCD=”ĻA£®
£Ø1£©ĒóÖ¤£ŗCDŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ3£¬CD=4£¬ĒóBDµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
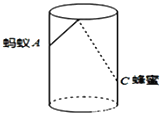
”¾ĢāÄæ”æČēĶ¼£¬Ō²ÖłŠĪ²£Į§±£¬øßĪŖ![]() £¬µ×ĆęÖܳ¤ĪŖ
£¬µ×ĆęÖܳ¤ĪŖ![]() £¬ŌŚ±ÄŚĄė±µ×
£¬ŌŚ±ÄŚĄė±µ×![]() µÄµć
µÄµć![]() “¦ÓŠŅ»µĪ·äĆŪ£¬“ĖŹ±Ņ»Ö»ĀģŅĻÕżŗĆŌŚ±Ķā±Ś£¬Ąė±ÉĻŃŲ
“¦ÓŠŅ»µĪ·äĆŪ£¬“ĖŹ±Ņ»Ö»ĀģŅĻÕżŗĆŌŚ±Ķā±Ś£¬Ąė±ÉĻŃŲ![]() Óė·äĆŪĻą¶ŌµÄµć
Óė·äĆŪĻą¶ŌµÄµć![]() “¦£¬ŌņĀģŅĻµ½“ļ·äĆŪµÄ×ī¶Ģ¾ąĄėĪŖ( )
“¦£¬ŌņĀģŅĻµ½“ļ·äĆŪµÄ×ī¶Ģ¾ąĄėĪŖ( )![]() .
.
A. 15B. ![]() C. 12D. 18
C. 12D. 18
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy£½2x+6½»xÖįÓŚA£¬½»yÖįÓŚB£®

£Ø1£©Ö±½ÓŠ“³öA£Ø”” ””£¬”” ””£©£¬B£Ø”” ””£¬”” ””£©£»
£Ø2£©ČēĶ¼1£¬µćEĪŖÖ±Ļßy£½x+2ÉĻŅ»µć£¬µćFĪŖÖ±Ļßy£½![]() xÉĻŅ»µć£¬ČōŅŌA£¬B£¬E£¬FĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ĒóµćE£¬FµÄ×ų±ź
xÉĻŅ»µć£¬ČōŅŌA£¬B£¬E£¬FĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ĒóµćE£¬FµÄ×ų±ź
£Ø3£©ČēĶ¼2£¬µćC£Øm£¬n£©ĪŖĻ߶ĪABÉĻŅ»¶Æµć£¬D£Ø©7m£¬0£©ŌŚxÖįÉĻ£¬Į¬½ÓCD£¬µćMĪŖCDµÄÖŠµć£¬ĒóµćMµÄׯ×ų±źyŗĶŗį×ų±źxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ö±½ÓŠ“³öŌŚµćCŅĘ¶Æ¹ż³ĢÖŠµćMµÄŌĖ¶ÆĀ·¾¶³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij·ž×°³§Éś²śŅ»ÖÖ¼ŠæĖŗĶTŠō£¬¼ŠæĖĆ漞¶Ø¼Ū120ŌŖ£¬TŠōĆ漞¶Ø¼Ū60ŌŖ£®³§·½ŌŚæŖÕ¹“ŁĻś»ī¶ÆĘŚ¼ä£¬ĻņæĶ»§Ģį¹©Į½ÖÖÓÅ»Ż·½°ø£ŗ¢ŁĀņŅ»¼ž¼ŠæĖĖĶŅ»¼žTŠō£»¢Ś¼ŠæĖŗĶTŠō¶¼°“¶Ø¼ŪµÄ80%ø¶æī£®ĻÖijæĶ»§ŅŖµ½øĆ·ž×°³§¹ŗĀņ¼ŠæĖ30¼ž£¬TŠō![]() ¼ž£Ø
¼ž£Ø![]() £¾30£©£®
£¾30£©£®
£Ø1£©ČōøĆæĶ»§°“·½°ø¢Ł¹ŗĀņ£¬Ščø¶æī”” ”” ŌŖ£ØÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾£©£»
ČōøĆæĶ»§°“·½°ø¢Ś¹ŗĀņ£¬Ščø¶æī”” ”” ŌŖ£ØÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©Čō![]() =40£¬Ķعż¼ĘĖćĖµĆ÷°“·½°ø¢Ł”¢·½°ø¢ŚÄÄÖÖ·½°ø¹ŗĀņ½ĻĪŖŗĻĖć£æ
=40£¬Ķعż¼ĘĖćĖµĆ÷°“·½°ø¢Ł”¢·½°ø¢ŚÄÄÖÖ·½°ø¹ŗĀņ½ĻĪŖŗĻĖć£æ
£Ø3£©ČōĮ½ÖÖÓÅ»Ż·½°øæÉĶ¬Ź±Ź¹ÓĆ£¬µ±![]() =40Ź±£¬ÄćÄÜøų³öŅ»ÖÖøüĪŖŹ”Ē®µÄ¹ŗĀņ·½°øĀš£æŹŌŠ“³öÄćµÄ¹ŗĀņ·½°ø£¬²¢ĖµĆ÷ĄķÓÉ£®
=40Ź±£¬ÄćÄÜøų³öŅ»ÖÖøüĪŖŹ”Ē®µÄ¹ŗĀņ·½°øĀš£æŹŌŠ“³öÄćµÄ¹ŗĀņ·½°ø£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČō½«“śŹżŹ½ÖŠµÄČĪŅāĮ½øö×ÖÄø½»»»£¬“śŹżŹ½²»±ä£¬Ōņ³ĘÕāøö“śŹżŹ½ĪŖĶźČ«¶Ō³ĘŹ½£¬Čē![]() ¾ĶŹĒĶźČ«¶Ō³ĘŹ½(“śŹżŹ½ÖŠ
¾ĶŹĒĶźČ«¶Ō³ĘŹ½(“śŹżŹ½ÖŠ![]() »»³Éb£¬b»»³É
»»³Éb£¬b»»³É![]() £¬“śŹżŹ½±£³Ö²»±ä).ĻĀĮŠČżøö“śŹżŹ½£ŗ¢Ł
£¬“śŹżŹ½±£³Ö²»±ä).ĻĀĮŠČżøö“śŹżŹ½£ŗ¢Ł![]() £»¢Ś
£»¢Ś![]() £»¢Ū
£»¢Ū![]() £®ĘäÖŠŹĒĶźČ«¶Ō³ĘŹ½µÄŹĒ£Ø £©
£®ĘäÖŠŹĒĶźČ«¶Ō³ĘŹ½µÄŹĒ£Ø £©
A.¢Ł¢ŚB.¢Ł¢ŪC.¢Ś¢ŪD.¢Ł¢Ś¢Ū
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½øö³¬ŹŠŅŌĶ¬ŃłµÄ¼Ūøń³öŹŪĶ¬ŃłµÄÉĢĘ·£¬µ«ø÷×ŌĶĘ³ö²»Ķ¬µÄÓÅ»Ż·½°ø£ŗŌŚ¼×³¬ŹŠĄŪ¼Ę¹ŗĪļ³¬¹ż100ŌŖŗ󣬳¬¹ż100ŌŖµÄ²æ·Ö°“80%ŹÕ·Ń£»ŌŚŅŅ³¬ŹŠĄŪ¼Ę¹ŗĪļ³¬¹ż50ŌŖŗ󣬳¬¹ż50ŌŖµÄ²æ·Ö°“90%ŹÕ·Ń.É芔Ć÷ŌŚĶ¬Ņ»³¬ŹŠĄŪ¼Ę¹ŗĪļ![]() ŌŖ£¬ĖūŌŚ¼×³¬ŹŠ¹ŗĪļŹµ¼Źø¶·Ń
ŌŖ£¬ĖūŌŚ¼×³¬ŹŠ¹ŗĪļŹµ¼Źø¶·Ń![]() (ŌŖ).ŌŚŅŅ³¬ŹŠ¹ŗĪļŹµ¼Źø¶·Ń
(ŌŖ).ŌŚŅŅ³¬ŹŠ¹ŗĪļŹµ¼Źø¶·Ń![]() (ŌŖ).
(ŌŖ).
(1)·Ö±šĒó³ö![]() £¬
£¬![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½.
µÄŗÆŹż¹ŲĻµŹ½.
(2)Ėę×ÅŠ”Ć÷ĄŪ¼Ę¹ŗĪļ½š¶īµÄ±ä»Æ£¬·ÖĪöĖūŌŚÄļŅ³¬ŹŠ¹ŗĪļøüŗĻĖć.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
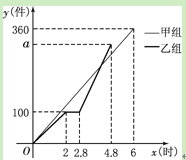
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½×鹤ČĖĶ¬Ź±¼Ó¹¤Ä³ÖÖĮć¼ž£¬ŅŅ×鹤×÷ÖŠÓŠŅ»“ĪĶ£²śøü»»Éč±ø£¬øü»»Éč±ø
ŗó£¬ŅŅ×éµÄ¹¤×÷Š§ĀŹŹĒŌĄ“µÄ2±¶£®Į½×éø÷×Ō¼Ó¹¤Įć¼žµÄŹżĮæ![]() (¼ž)ÓėŹ±¼ä
(¼ž)ÓėŹ±¼ä![]() (Ź±)µÄŗÆŹżĶ¼
(Ź±)µÄŗÆŹżĶ¼
ĻóČēĶ¼ĖłŹ¾£®
£Ø1£©Ēó¼××é¼Ó¹¤Įć¼žµÄŹżĮæyÓėŹ±¼ä![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®£Ø2·Ö£©
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®£Ø2·Ö£©
£Ø2£©ĒóŅŅ×é¼Ó¹¤Įć¼ž×ÜĮæ![]() µÄÖµ£®£Ø3·Ö£©
µÄÖµ£®£Ø3·Ö£©
£Ø3£©¼×”¢ŅŅĮ½×é¼Ó¹¤³öµÄĮć¼žŗĻŌŚŅ»Ęš×°Ļ䣬Ćæ¹»300¼ž×°Ņ»Ļ䣬Įć¼ž×°ĻäµÄŹ±¼äŗöĀŌ²»¼Ę£¬Ēó¾¹ż¶ą³¤Ź±¼äĒ”ŗĆ×°ĀśµŚ1Ļä£æŌŁ¾¹ż¶ą³¤Ź±¼äĒ”ŗĆ×°ĀśµŚ2Ļä£æ£Ø5·Ö£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB£½4£¬AD£½5£¬AD”¢AB”¢BC·Ö±šÓė”ŃOĻąĒŠÓŚE”¢F”¢GČżµć£¬¹żµćD×÷”ŃOµÄĒŠĻß½»BCÓŚµćM£¬ŌņDMµÄ³¤ĪŖ(””””)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com