
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
【答案】(1) 2015至2017年的平均增长率为37.5%;(2)单人间的数量是28间;(3)该校的寝室建成后最多可供596名师生住宿.
【解析】
(1)可设2015至2017年的平均增长率是x,根据等量关系:2015年学校寝室数×(1+平均增长率)2=2017年学校寝室数,列出方程求解即可;
(2)设双人间的数量为y间,则四人间的数量为5y间,根据不等量关系:单人间的数量在20至于30之间(包括20和30),列出不等式,再根据整数的性质即可求解;
(3)由于四人间的数量是双人间的5倍,可知四人间和双人间的数量是5+1=6的倍数,找到150~160间6的最大倍数,再进一步求出双人间和四人间的数量,以及单人间的数量,从而求解.
(1)设2015至2017年的平均增长率是x,
依题意有64(1+x)2=121,
解得x1=0.375,x2=-2.375.
故2015至2017年的平均增长率为37.5%;
(2)设双人间的数量为y间,则四人间的数量为5y间,
依题意有20≤600-2y-4×5y≤30,
解得25![]() ≤y≤26
≤y≤26![]() ,
,
∵y为整数,
∴y=26,
600-2y-4×5y=600-52-520=28.
故单人间的数量是28间;
(3)由于四人间的数量是双人间的5倍,则四人间和双人间的数量是5+1=6的倍数,双人间与四人间总数量在150~160之间.
∵150~160间6的最大倍数是156,
∴双人间156÷6=26(间),
四人间的数量26×5=130(间),单人间180-156=24(间),
24+26×2+130×4=596(名).
答:该校的寝室建成后最多可供596名师生住宿.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】发现与探索
你能求 x 1x2019 x2018 x2017 x 1 的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形手.先分别计算下列各式的值:
① x 1 x 1 x2 1 ;
② x 1x2 x 1 x3 1 ;
③ x 1x3 x2 x 1 x4 1 ;
由此我们可以得到:
x 1x2019 x2018 x2017 x 1 ; 请你利用上面的结论,完成下面两题的计算:
(1)32019 32018 32017 3 1 ;
(2)250 249 248 2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
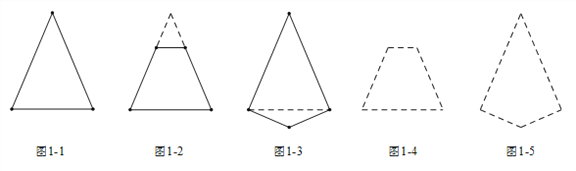
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有________条对称轴,非正方形的长方形有________条对称轴,等边三角形有___________条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
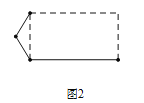
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测点O处测得该船位于北偏东60°的方向,则该船航行的距离为( )
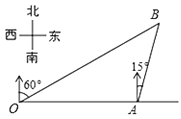
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠EOD=90°;②∠COE=∠AOD;③∠AOE+∠DOC=180![]() ;④互余的角有4对.其中正确的有( )
;④互余的角有4对.其中正确的有( )
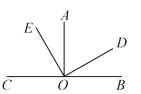
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
①以点A为圆心,小于AC的长为半径.画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于![]() EF的长为半径画弧,两弧相交于点G;
EF的长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D,则∠ADC的度数为________.

【答案】65°
【解析】由题意可知,所作的射线AG是∠BAC的角平分线.
∵在△ABC中,∠C=90°,∠ABC=40°,
∴∠BAC=180°-90°-40°=50°,
∴∠CAD=![]() ∠BAC=25°,
∠BAC=25°,
∴∠ADC=180°-90°-25°=65°.
【题型】填空题
【结束】
13
【题目】如图所示,已知线段AB,∠α,∠β,分别过A、B作∠CAB=∠α,∠CBA=∠β.(不写作法,保留作图痕迹)


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值 ![]() ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.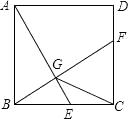
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com