
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
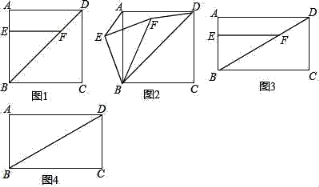
①如图1,请直接写出AE与DF的数量关系 ;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由.
(2)若四边形ABCD为矩形,BC=mAB,其他条件都不变.
①如图3,猜想AE与DF的数量关系并说明理由;
②将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图4中画出草图,并直接写出AE′和DF′的数量关系.
【答案】(1)DF=![]() AE;DF=
AE;DF=![]() AE;(2)DF=
AE;(2)DF=![]() MF=
MF=![]() AE;DF′=
AE;DF′=![]() AE′.
AE′.
【解析】
(1)①利用正方形的性质得△ABD为等腰直角三角形,则BD=![]() AB,再证明△BEF为等腰直角三角形得到BF=
AB,再证明△BEF为等腰直角三角形得到BF=![]() BE,所以BD-BF=
BE,所以BD-BF=![]() AB-
AB-![]() BE,从而得到DF=
BE,从而得到DF=![]() AE;
AE;
②利用旋转的性质得∠ABE=∠DBF,结合![]() =
=![]() , 则根据相似三角形的判定可得到△ABE∽△DBF,所以
, 则根据相似三角形的判定可得到△ABE∽△DBF,所以![]() =
=![]() ;
;
(2)①作FM⊥AD,垂足为M.依据勾股定理可得Rt△ABD中,BD=![]() =
=![]() AB,再根据△DMF∽△ABD,可得
AB,再根据△DMF∽△ABD,可得![]() =
=![]() ,即可得出DF=
,即可得出DF=![]() AE;
AE;
②依据△BEF∽△BAD,可得![]() =
=![]() ,进而得出
,进而得出![]() =
=![]() ,即可得出△ABE′∽△DBF′,进而得到
,即可得出△ABE′∽△DBF′,进而得到![]() =
=![]() ,即DF′=
,即DF′=![]() AE′.
AE′.
解:(1)①∵四边形ABCD为正方形,
∴△ABD为等腰直角三角形,
∴BD=![]() AB,
AB,
∵EF⊥AB,
∴△BEF为等腰直角三角形,
BF=![]() BE,
BE,
∴BD﹣BF=![]() AB﹣
AB﹣![]() BE,
BE,
即DF=![]() AE,
AE,
故答案为:DF=![]() AE;
AE;
②DF=![]() AE.理由如下:
AE.理由如下:
∵△EBF绕点B逆时针旋转到图2所示的位置,
∴∠ABE=∠DBF,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∴△ABE∽△DBF,
∴![]() =
=![]() ,
,
即AE与DF的数量关系是:DF=![]() AE;
AE;
(2)①AE与DF的数量关系是:DF=![]() AE;
AE;
理由:在图3中,作FM⊥AD,垂足为M.
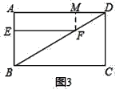
∵∠A=∠AEF=∠AMF=90°,
∴四边形AEFM是矩形,
∴FM=AE,
∵AD=BC=mAB,
∴Rt△ABD中,BD=![]() =
=![]() AB,
AB,
∵MF∥AB,
∴△DMF∽△ABD,
∴![]() =
=![]() ,
,
∴DF=![]() MF=
MF=![]() AE;
AE;
②AE′和DF′的数量关系:DF'=![]() AE'.
AE'.
如图3,∵四边形ABCD为矩形,
∴AD=BC=mAB,
∴BD=![]() =
=![]() AB,
AB,
∵EF⊥AB,
∴EF∥AD,
∴△BEF∽△BAD,
∴![]() ,
,
∴![]() =
=![]() ,
,
如图4,∵△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',

∴∠ABE′=∠DBF′,BE′=BE,BF′=BF,
∴![]() =
=![]() ,
,
∴△ABE′∽△DBF′,
∴![]() =
=![]() ,
,
即DF′=![]() AE′.
AE′.


科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中A(3,2),B(4,3),C(1,1).
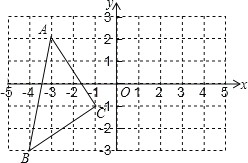
(1)在图中作出△ABC关于y轴对称图形△A1B1C1;
(2)写出A1、B1、C1的坐标分别是A1(___,___),B1(___,___),C1(___,___);
(3)△ABC的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
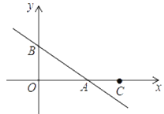
【题目】如图,直线 ![]() 分别交x轴、y轴于A、B两点,已知点C坐标为(6,0),若直线AB上存在点P,使∠OPC=90°,则m的取值范围是________。
分别交x轴、y轴于A、B两点,已知点C坐标为(6,0),若直线AB上存在点P,使∠OPC=90°,则m的取值范围是________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AD 为△ ABC 的中线, BE 为△ ABD 的中线.
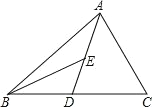
(1)∠ ABE=15°,∠ BED=55°,求∠ BAD 的度数;
(2)作△ BED 的边 BD 边上的高;
(3)若△ ABC 的面积为 20, BD=2.5,求△ BDE 中 BD 边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
(1)求∠EAF的度数;
(2)如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.

查看答案和解析>>
科目:初中数学 来源: 题型:
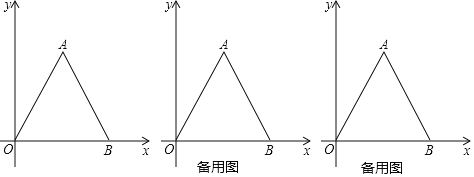
【题目】如图,在平面直角坐标系中,等边三角形△ABO的边长为4.
(1)求点A的坐标.
(2)若点P从点O出发以每秒1个单位的速度沿x轴正方向运动,运动时间为t秒,△PAB的面积为S,求S与t的关系式,并直接写出t的范围.
(3)在(2)的条件下,当点P在点B的右侧时,若S=![]() ,在平面内是否存在点Q,使点P、Q、A、B围成的四边形是平行四边形?若存在,求出点Q坐标;若不存在,请说明理由.
,在平面内是否存在点Q,使点P、Q、A、B围成的四边形是平行四边形?若存在,求出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
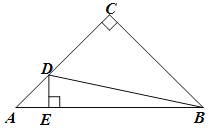
【题目】如图,Rt△ABC中, ![]() ,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为
,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为![]() cm,BD长为
cm,BD长为![]() cm(当D与A重合时,
cm(当D与A重合时, ![]() =4;当D与B重合时
=4;当D与B重合时![]() =0).
=0).
小云根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小云的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
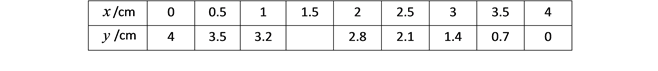
补全上面表格,要求结果保留一位小数.则![]() __________.
__________.
(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从丙、丁两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达丁地后,乙继续前行.设出发![]() 后,两人相距
后,两人相距![]() ,图中折线表示从两人出发至乙到达丙地的过程中
,图中折线表示从两人出发至乙到达丙地的过程中![]() 与
与![]() 之间的函数关系.根据图中信息,求:
之间的函数关系.根据图中信息,求:
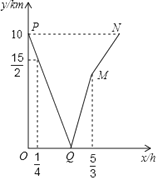
(1)点![]() 的坐标,并说明它的实际意义;
的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com