
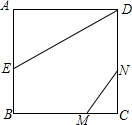
 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似? 分析 根据AE=EB,△AED中AD=2AE,所以在△MNC中,分CM与AE和AD是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系,然后利用勾股定理列式计算即可.
解答 解:∵AE=EB,
∴AD=2AE,
又∵△AED与以M、N、C为顶点的三角形相似,
∴分两种情况:
①CM与AD是对应边时,CM=2CN,
∴CM2+CN2=MN2=1,
即CM2+$\frac{1}{4}$CM2=1,
解得:CM=$\frac{2\sqrt{5}}{5}$;
②CM与AE是对应边时,CM=$\frac{1}{2}$CN,
∴CM2+CN2=MN2=1,
即CM2+4CM2=1,
解得:CM=$\frac{\sqrt{5}}{5}$.
综上所述:当CM为$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$时,△AED与△CMN相似.
点评 本题考查了正方形的性质、勾股定理、相似三角形的判定;主要利用相似三角形对应边成比例的性质和直角三角形勾股定理求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (3,2) | C. | (-2,3) | D. | (2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
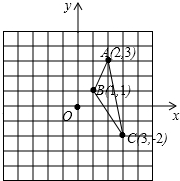 如图,利用关于坐标轴对称的点的坐标特点.
如图,利用关于坐标轴对称的点的坐标特点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).
如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com