
分析 (1)先去括号,把各二次根式化为最简二次根式,然后合并即可.
(2)首先利用完全平方公式计算,并化简二次根式,求出答案.
解答 解:(1)原式=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-2$\sqrt{6}$,
=-$\frac{3}{4}$$\sqrt{2}$;
(2)原式=12-4$\sqrt{18}$+6+(3$\sqrt{6}$+$\sqrt{6}$)$÷\sqrt{3}$,
=12-12$\sqrt{2}$+6+4$\sqrt{2}$,
=18-8$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了完全平方公式的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
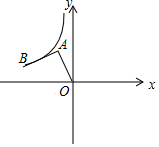 如图,在平面直角坐标系中,点A(-1,2),将AO绕点A顺时针旋转90°,点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上,则k的值为-3.
如图,在平面直角坐标系中,点A(-1,2),将AO绕点A顺时针旋转90°,点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上,则k的值为-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一大一小的两个可以自由转动的转盘,甲盘被平均分成6等份,乙盘被平均分成4等份,每个转盘均被涂上红、黄、蓝三种颜色,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色,小明与小颖参与游戏;小明转动甲盘,小颖转动乙盘.
如图是一大一小的两个可以自由转动的转盘,甲盘被平均分成6等份,乙盘被平均分成4等份,每个转盘均被涂上红、黄、蓝三种颜色,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色,小明与小颖参与游戏;小明转动甲盘,小颖转动乙盘.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
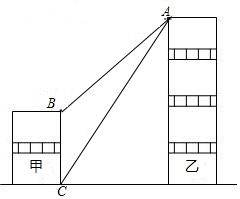 小颖站在自家阳台的A处用测角仪观察对面的商场,如图,在A处测得商场楼顶B点的俯角为45°,商场楼底C点的俯角为60°,若商场高17.6米,小颖家所在楼房每层楼的平均高度为3米,则小颖家住在几楼?小颖家与商场相距多少米?(结果保留整数,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
小颖站在自家阳台的A处用测角仪观察对面的商场,如图,在A处测得商场楼顶B点的俯角为45°,商场楼底C点的俯角为60°,若商场高17.6米,小颖家所在楼房每层楼的平均高度为3米,则小颖家住在几楼?小颖家与商场相距多少米?(结果保留整数,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com