
【题目】如图,⊙O过A,C,D三点,过D作DB∥AC,且AC=AD,CD=CB.
(1)求证:BC为⊙O的切线;
(2)若cosB=![]() ,求
,求![]() 的值.
的值.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OC,OD根据AC∥BD,可证∠ACD=∠CDB,通过AC=AD,CD=CB可证
∠ACD=∠ADC,∠CDB=∠CBD,进而可证∠DCB=∠A,∠DOC=2∠A,∠DOC=2∠DCB
求出∠OCD+∠DCB=90°即可,
(2)作CM⊥BD,由BC=CD可证BM=DM再由cos∠B= ![]()
(1)连接OC、OD,
∵AC∥BD,
∴∠ACD=∠CDB,
∵AC=AD,CD=CB,
∴∠ACD=∠ADC,∠CDB=∠CBD,
∴∠DCB=∠A,
∵∠DOC=2∠A,
∴∠DOC=2∠DCB,
设∠DCB=x,∠OCD=y,则∠DOC=2x,
△OCD中,2x+2y=180,
x+y=90,
即∠OCD+∠DCB=90°,
∴BC为⊙O的切线;
(2)解:过C作CM⊥BD于M,则BM=DM,
cos∠B= ![]() ,
,
设BM=2x,BC=5x,
∴![]() =
= ![]() .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张三角形纸片ABC,其中∠BAC=60°,BC=6,点D是BC边上一动点,将BD,CD翻折使得B′,C′分别落在AB,AC边上,(B与B′,C与C′分别对应),点D从点B运动至点C,△B′C′D面积的大小变化情况是( )

A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
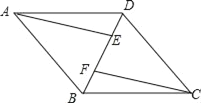
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
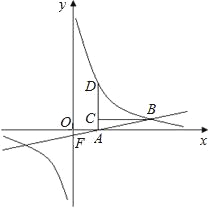
【题目】如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求该双曲线的解析式;
(2)求△OFA的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com