
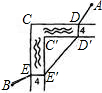
 如图,护城河在CC'处直角转弯,宽度保持为4米.从A处往B处,经过2座桥:DD',EE'.设护城河是东西一南北方向的,A、B在东西方向上相距64米,南北方向上相距84米.恰当地架桥可使AD、D'E′、EB的路程最短.这个最短路程为________米.
如图,护城河在CC'处直角转弯,宽度保持为4米.从A处往B处,经过2座桥:DD',EE'.设护城河是东西一南北方向的,A、B在东西方向上相距64米,南北方向上相距84米.恰当地架桥可使AD、D'E′、EB的路程最短.这个最短路程为________米.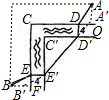 解:如图,作AQ⊥CD,在AQ上截取AA′=DD′;作BF⊥CE,在BF上截取BB′=EE′,
解:如图,作AQ⊥CD,在AQ上截取AA′=DD′;作BF⊥CE,在BF上截取BB′=EE′, =100米,
=100米,

科目:初中数学 来源: 题型:解答题
 如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?
如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com