
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得
不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得![]() 成立的一对数m,n为“相伴数对”,记为(m,n).
成立的一对数m,n为“相伴数对”,记为(m,n).
(1)若(m,1)是“相伴数对”,则m=_____;
(2)(m,n)是“相伴数对”,则代数式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值为_____.
(6﹣12n﹣15m)]的值为_____.
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( ) 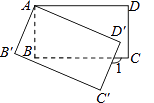
A.68°
B.20°
C.28°
D.22°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( ) 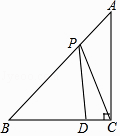
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“*”是新规定的这样一种运算法则:a*b=a2+2ab,比如3*(﹣2)=32+2×3×(﹣2)=﹣3
(1)试求2*(﹣3)的值;
(2)若2*x=2,求x的值;
(3)若(﹣2)*(1*x)=x+9,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了形式多样的“阳光体育运动”活动,小李对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1 和图2,并且“乒乓球”对应的∠AOC=108°.
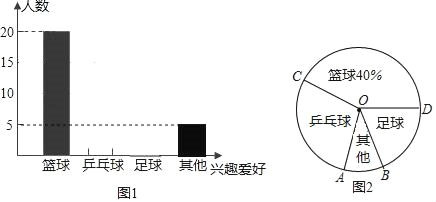
(1)求该班级的学生人数;
(2)在图1中将“乒乓球”和“足球”项目的图形补充完整;
(3)在图2中求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.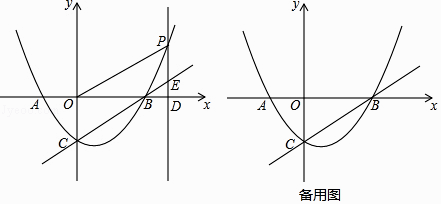
(1)求抛物线解析式;
(2)若点P在第一象限内,当OD=4PE时,求四边形POBE的面积;
(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在上,直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蚂蚁从点O出发,在一条直线上来回爬行.假定向右爬行的路程记为正数,向左爬行的路程记为负数,则爬过的各段路程依次记为(单位:cm):+5,-3,+10,-8,-6,+12,-10.
![]()
(1)蚂蚁最后是否回到出发点O?
(2)蚂蚁离开出发点O最远是多少?
(3)在爬行过程中,如果每爬行1奖励一粒糖,那么蚂蚁一共得到多少粒糖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段 AB 的长为 10cm,C 是直线 AB 上一动点,M 是线段 AC的中点,N 是线段 BC 的中点.
(1)若点 C 恰好为线段 AB 上一点,求MN等于多少cm;
(2)猜想线段 MN 与线段 AB 长度的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com