
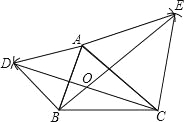
【题目】以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD.(尺规作图,不写作法,保留作图痕迹)
【答案】作图与证明见解析
【解析】
试题分析:分别以A、B为圆心,AB长为半径画弧,两弧交于点D,连接AD,BD,同理连接AE,CE,如图所示,由三角形ABD与三角形ACE都是等边三角形,得到三对边相等,两个角相等,都为60度,利用等式的性质得到夹角相等,利用SAS得到三角形CAD与三角形EAB全等,利用全等三角形的对应边相等即可得证.
试题解析:如图所示:
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
∵在△CAD和△EAB中,
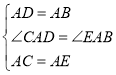 ,
,
∴△CAD≌△EAB(SAS),
∴BE=CD.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】某种濒危动物的数量每年以10%的速度减少,n年后该动物数量p与现有数量m之间的关系是p=m(1-10%)n.已知该动物现有数量为8000只,则3年后该动物还有( )
A. 5832 B. 5823 C. 4000 D. 5000
查看答案和解析>>
科目:初中数学 来源: 题型:
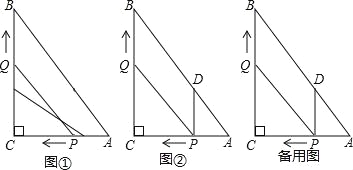
【题目】如图①,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,点P,Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t妙(t≥0).
(1)若三角形CPQ是等腰三角形,求t的值.
(2)如图②,过点P作PD∥BC,交AB于点D,连接PQ;
①是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度.
②当t取何值时,△CPQ的外接圆面积的最小?并且说明此时△CPQ的外接圆与直线AB的位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,△ABC中,DE∥BC,AD:DB=1:2,下列选项正确的是( )
A.DE:BC=1:2
B.AE:AC=1:3
C.BD:AB=1:3
D.S△ADE:S△ABC=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
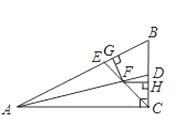
【题目】如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,且FG⊥AB于G,FH⊥BC于H.
(1)求证:∠BEC=∠ADC;
(2)请你判断并FE与FD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象只经过第一、二、三象限,则( )
A. k<0,b>0 B. k>0,b>0 C. k>0,b<0 D. k<0,b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快赣州的交通发展,将建设赣州至深圳的高速铁路,项目总投资为641.3亿元,用科学记数法表示641.3亿元为( )元.
A.6.41×102
B.641×108
C.6.41×1010
D.6.41×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com