



 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
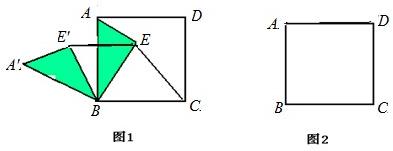
 小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时,由于EA、EB、EC比较分散,不便解决.于是将△ABE绕点B逆时针旋转60°得△A′BE′,连接EE′.
小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时,由于EA、EB、EC比较分散,不便解决.于是将△ABE绕点B逆时针旋转60°得△A′BE′,连接EE′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
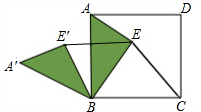 小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时,由于EA、EB、EC比较分散,不便解决.于是将△ABE绕点B逆时针旋转60°得△A′BE′,连接EE′.
小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时,由于EA、EB、EC比较分散,不便解决.于是将△ABE绕点B逆时针旋转60°得△A′BE′,连接EE′.查看答案和解析>>
科目:初中数学 来源:2012-2013学年江西省抚州市临川二中九年级(上)第一次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年河南省商丘市外国语中学中考数学模拟试卷(三)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com