
【题目】已知锐角△ABC内接于圆O,D为弧AC上一点,分别连接AD、BD、CD,且∠ACB=90°﹣![]() ∠BAD.
∠BAD.
(1)如图1,求证:AB=AD;
(2)如图2,在CD延长线上取点E,连接AE,使AE=AD,过E作EF垂直BD的延长线于点F,过C作CG⊥EC交EF延长线于点G,设圆O半径为r,求证:EG=2r;
(3)如图3,在(2)的条件下,连接DG,若AC=BC,DE=4CD,当△ACD的面积为10时,求DG的长度.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)欲证明AB=AD,只要证明∠ABD=∠ADB即可;(2)如图2中,连接BE交AC于L,连接AO,延长AO交BD于J,交BE于T,连接CO,延长CO交⊙O于K,连接BK.想办法证明△CBK≌△ECG(AAS)可得结论;(3)如图3中,在图2的基础上作AH⊥DE于H.假设CD=k,DE=4k,则CE=CB=CA=5k,利用勾股定理求出AH,再利用三角形的面积公式求出K的值,再求出EG,CG即可解决问题.
(1)证明:如图1中,

∵∠∠ADB=∠ACB,∠ACB=90°﹣![]() ∠BAD,
∠BAD,
∴∠ADB=90°﹣![]() BAD,
BAD,
∵∠ABD=180°﹣∠BAD﹣(90°﹣![]() ∠BAD)=90°﹣
∠BAD)=90°﹣![]() ∠BAD,
∠BAD,
∴∠ABD=∠ADB,
∴AB=AD.
(2)证明:如图2中,连接BE交AC于L,连接AO,延长AO交BD于J,交BE于T,连接CO,延长CO交⊙O于K,连接BK.

∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠ADC=180°,∠ADC+∠ABC=180°,
∴∠ADE=∠ABC=∠AED,
∵AB=AD,
∴![]() ,
,
∴∠ACB=∠ACE,AJ⊥BD,
∵AC=AC,
∴△ACB≌△ACE(AAS),
∴CB=CE,
∵AB=AE,
∴AC⊥BE,
∴∠ALB=∠AJB=90°,
∵∠ATL=∠BTJ,
∴∠TAL=∠TBJ,
∵AB=AD=AE,
∴∠BED=![]() ∠BAD=∠BAJ,
∠BAD=∠BAJ,
∵∠EDF=∠DBE+∠DEB,
∴∠EDF=∠BAC,
∵∠K=∠BAC,
∴∠K=∠EDF,
∵CG⊥CE.EG⊥BF,
∴∠DFE=∠GCG=90°,
∵∠DEF+∠EDF=90°,∠DEF+∠G=90°,
∴∠G=∠EDF=∠K,
∵∠CBK=∠GCE=90°,
∴△CBK≌△ECG(AAS),
∴EG=CK=2r,
(3)解:如图3中,在图2的基础上作AH⊥DE于H.

∵DE=4CD,
∴可以假设CD=k,DE=4k,则CE=CB=CA=5k,
∵AE=AD,AH⊥DE,
∴DH=EH=2k,CH=CD+DH=3k,
∴AH=![]() ,
,
AD=![]()
∵S△ACD=![]() CDAH=
CDAH=![]() k4k=10,
k4k=10,
∴k=![]() (负根舍弃),
(负根舍弃),
∴CD=![]() ,AC=BC=EC=5
,AC=BC=EC=5![]() ,AD=AB=10,
,AD=AB=10,
设CK交AB于J,OA=OC=r,则BJ=AJ=5,CJ=![]()
在Rt△AOJ中,则有r2=52+(10﹣r)2,
解得r=![]() ,
,
∴EG=2r=![]() ,
,
∴CG=![]()
∴DG=![]()


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]()
(1)求一次函数的解析式
(2)已知双曲线在第一象限上有一点到![]() 到
到![]() 轴的距离为3,求
轴的距离为3,求![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.

(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内有一古塔AB,在塔的北面有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高3米的影子CD;而当光线与地面的夹角是45°时,塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a>![]() AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.
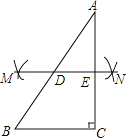
(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(-![]() ,y1),B(-1,y2),C(1,y3)为二次函数y=-x2-4x+5的图象上的三点,则y1,y2,y3的大小关系是( )
,y1),B(-1,y2),C(1,y3)为二次函数y=-x2-4x+5的图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3B.y3<y2<y1C.y3<y1<y2D.y2<y1<y3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com