
 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x s,四边形APQC的面积为y mm2.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x s,四边形APQC的面积为y mm2.分析 (1)利用两个直角三角形的面积差求得答案即可;
(2)利用线段的长度与运动速度建立不等式得出答案即可;
(3)利用(1)的函数建立方程求解判断即可.
解答 解:(1)∵出发时间为t,点P的速度为2mm/s,点Q的速度为4mm/s,
∴PB=12-2t,BQ=4t,
∴y=$\frac{1}{2}$×12×24-$\frac{1}{2}$×(12-2t)×4t
=4t2-24t+144.
(2)∵t>0,12-2t>0,
∴0<t<6.
(3)不能,
4t2-24t+144=172,
解得:t1=7,t2=-1(不合题意,舍去)
因为0<t<6.所以t=7不在范围内,
所以四边形APQC的面积不能等于172mm2.
点评 此题考查二次函数的实际运用,一元二次方程的实际运用,掌握三角形的面积计算方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
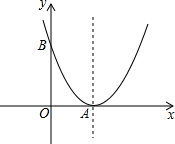 如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).
如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
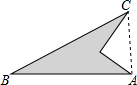 一个零件的形状如图所示,按规定∠BAC应为直角,工人师傅测得∠ADC=90°,AD=6,CD=8,AB=24,BC=26,请你帮他看一下,这个零件符合要求吗?为什么.
一个零件的形状如图所示,按规定∠BAC应为直角,工人师傅测得∠ADC=90°,AD=6,CD=8,AB=24,BC=26,请你帮他看一下,这个零件符合要求吗?为什么.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE,CE
如图,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE,CE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com