
(8分) 已知:在矩形 中,
中,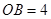 ,
, .分别以
.分别以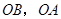 所在直线为
所在直线为 轴和
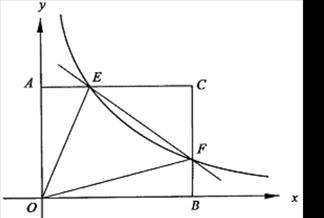
轴和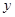 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.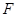 是边
是边 上的一个动点(不与
上的一个动点(不与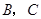 重合),过
重合),过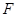 点的反比例函数
点的反比例函数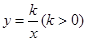 的图象与
的图象与 边交于点
边交于点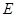 .
.
1.(1)求证: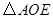 与
与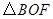 的面积相等;
的面积相等;
2.(2)记 ,求当
,求当 为何值时,
为何值时, 有最大值,最大值为多少?
有最大值,最大值为多少?
3.(3)请探索:是否存在这样的点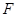 ,使得将
,使得将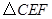 沿
沿 对折后,
对折后,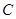 点恰好落在
点恰好落在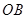 上?若存在,求出点
上?若存在,求出点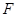 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
(8分) 已知:在矩形![]() 中,
中,![]() ,
,![]() .分别以
.分别以![]() 所在直线为
所在直线为![]() 轴和
轴和![]() 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系. 是边
是边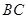 上的一个动点(不与
上的一个动点(不与 重合),过
重合),过 点的反比例函数
点的反比例函数 的图象与
的图象与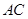 边交于点
边交于点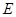 .
.

1.(1)求证:![]() 与
与![]() 的面积相等;
的面积相等;
2.(2)记![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 有最大值,最大值为多少?
有最大值,最大值为多少?
3.(3)请探索:是否存在这样的点![]() ,使得将
,使得将![]() 沿
沿![]() 对折后,
对折后,![]() 点恰好落在
点恰好落在![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 中,
中, ,
, .分别以
.分别以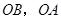 所在直线为
所在直线为 轴和
轴和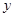 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.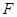 是边
是边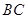 上的一个动点(不与
上的一个动点(不与 重合),过
重合),过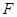 点的反比例函数
点的反比例函数 的图象与
的图象与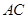 边交于点
边交于点 .
.
 与
与 的面积相等;
的面积相等; ,求当
,求当 为何值时,
为何值时,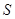 有最大值,最大值为多少
有最大值,最大值为多少 ?
?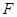 ,使得将
,使得将 沿
沿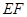 对折后,
对折后, 点恰好落在
点恰好落在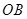 上?若存在,求出点
上?若存在,求出点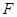 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2012届浙江省桐乡市河山镇中学学校九年级第一学期期末调研测试数学卷 题型:解答题
(8分)已知:在矩形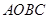 中,
中,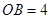 ,
,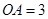 .分别以
.分别以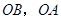 所在直线为
所在直线为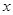 轴和
轴和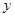 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.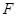 是边
是边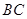 上的一个动点(不与
上的一个动点(不与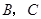 重合),过
重合),过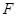 点的反比例函数
点的反比例函数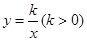 的图象与
的图象与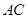 边交于点
边交于点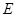 .
.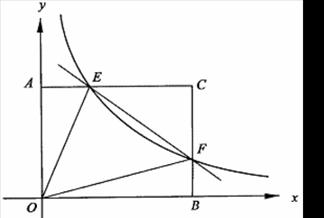
【小题1】(1)求证: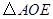 与
与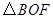 的面积相等;
的面积相等;
【小题2】(2)记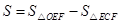 ,求当
,求当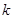 为何值时,
为何值时,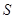 有最大值,最大值为多少
有最大值,最大值为多少 ?
?
【小题3】(3)请探索:是否存在这样的点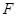 ,使得将
,使得将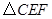 沿
沿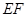 对折后,
对折后,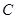 点恰好落在
点恰好落在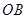 上?若存在,求出点
上?若存在,求出点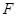 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:在矩形![]() 中,
中,![]() ,
,![]() .分别以
.分别以![]() 所在直线为
所在直线为![]() 轴和
轴和![]() 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.![]() 是边
是边![]() 上的一个动点(不与
上的一个动点(不与![]() 重合),过
重合),过![]() 点的反比例函数
点的反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() .
.
(1)求证:![]() 与
与![]() 的面积相等;
的面积相等;
(2)记![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 有最大值,最大值为多少?
有最大值,最大值为多少?
(3)请探索:是否存在这样的点![]() ,使得将
,使得将![]() 沿
沿![]() 对折后,
对折后,![]() 点恰好落在
点恰好落在![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com