
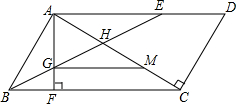
 已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.分析 (1)根据等边对等角以及平行线的性质,即可得到∠1=∠2=$\frac{1}{2}$∠ABC,再根据平行四边形ABCD中,∠D=50°=∠ABC,可得出∠EBC的度数;
(2)过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°,先根据AAS判定△BPG≌△BFG,得到PG=GF,根据矩形GFNM中GF=MN,即可得出PG=NM,进而判定△PAG≌△NCM(AAS),可得AG=CM,再根据等角对等边得到AH=AG,即可得到结论.
解答 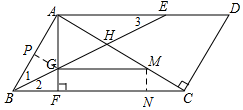 解:(1)∵AB=AE,
解:(1)∵AB=AE,
∴∠1=∠3,
∵AE∥BC,
∴∠2=∠3,
∴∠1=∠2=$\frac{1}{2}$∠ABC,
又∵平行四边形ABCD中,∠D=50°,
∴∠ABC=50°,
∴∠EBC=25°;
(2)证明:如图,过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°,
由(1)可得,∠1=∠2,
∵AF⊥BC,
∴∠BPG=∠BFG=90°,
在△BPG和△BFG中,
$\left\{\begin{array}{l}{∠CNM=∠APG}\\{∠1=∠2}\\{BG=BG}\end{array}\right.$,
∴△BPG≌△BFG(AAS),
∴PG=GF,
又∵矩形GFNM中,GF=MN,
∴PG=NM,
∵AC⊥CD,CD∥AB,
∴∠BAC=90°=∠AFB,
即∠PAG+∠ABF=∠NCM+∠ABC=90°,
∴∠PAG=∠NCM,
在△PAG和△NCM中,
$\left\{\begin{array}{l}{∠PAG=∠NCM}\\{∠CNM=∠APG}\\{PG=NM}\end{array}\right.$,
∴△PAG≌△NCM(AAS),
∴AG=CM,
∵∠1=∠2,∠BAH=∠BFG,
∴∠AHG=∠FGB=∠AGH,
∴AG=AH,
∴AH=CM.
点评 本题主要考查了平行四边形的性质,全等三角形的判定与性质以及等腰三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,依据全等三角形的对应边相等进行推理.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
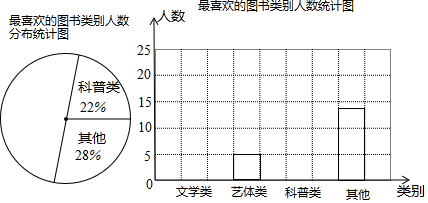
| 图书类别 | 画记 | 人数 | 百分比 |
| 文学类 | |||
| 艺体类 | 正 | 5 | |
| 科普类 | 正正$\overline{\;}$ | 11 | 22% |
| 其他 | 正正 | 14 | 28% |
| 合计 | a | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
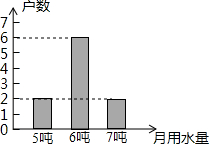 2016年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法错误的是( )
2016年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法错误的是( )| A. | 众数是6 | B. | 中位数是6 | C. | 平均数是6 | D. | 方差是4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解这个不等式组,并将解集在数轴上表示出来:
解这个不等式组,并将解集在数轴上表示出来:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=\frac{4}{3}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
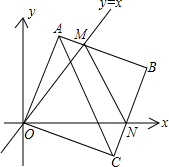 如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.
如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com