
【题目】如图,在正方形 ABCD 中,点 E 是对角线 BD 上一动点,AE 的延长线交 CD 于点 F,交 BC 的延长线于点 G,M 是 FG 的中点.
(1)求证: ∠DAE=∠DCE;
(2)判断线段 CE 与 CM 的位置关系,并证明你的结论;
(3)当![]() ,并且
,并且![]() 恰好是等腰三角形时,求 DE 的长.
恰好是等腰三角形时,求 DE 的长.

【答案】(1)证明见解析;(2)EC⊥MC, 理由见解析;(3)DE=![]()
【解析】(1)首先根据正方形的性质可得AD=CD,∠ADB=∠CDB=45°,再有DE是公共边,可以利用SAS判定△ADE和△CDE全等;
(2)由AD∥BG得∠DAE=∠G,由M 是 FG 的中点得MC=MG=MF,可求得∠DCE=∠MCG,由∠FCG=∠MCG+∠FCM=90°可得∠ECM=∠DCE+∠FCM=90°,从而EC⊥MC;
(3)由题意可知CE=CG,由∠MCG=∠G,∠EMC=2∠G可求得∠G=30°. 过点 E 作 EH⊥AD 于 H,设 EH=x,利用勾股定理表示出AH,根据AD=AH+DH列方程求出x,进而可求出DE的长.
(1)证明:∵四边形 ABCD 是正方形,
∴∠ADE=∠CDE,AD=CD, 在△ADE 与△CDE,
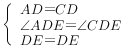 ,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE;
(2)EC⊥MC, 理由如下:
∵AD∥BG,
∴∠DAE=∠G,
∵M 是 FG 的中点,
∴MC=MG=MF,
∴∠G=∠MCG, 又∵∠DAE=∠DCE,
∴∠DCE=∠MCG,
∵∠FCG=∠MCG+∠FCM=90°,
∴∠ECM=∠DCE+∠FCM=90°,
∴EC⊥MC;
(3)∵∠FCG=90°,
∴∠ECG 一定是钝角,
∴△CEG 若为等腰三角形必有 CE=CG,
∴∠CEM=∠G,
∵![]() ,
,
∴∠MCG=∠G, 又∵∠EMC=∠MCG+∠G,
∴∠EMC=2∠G,
∵∠ECM=90°,
∴∠CEM+∠EMC=90°,
∴∠G+2∠G=90°,
∴∠G=30°,
∴∠AFD=∠CFG=90°-∠G=90°-30°=60°,
∴∠DAE=90°-∠AFD=90°-60°=30°, 过点 E 作 EH⊥AD 于 H,设 EH=x,
∴∠EHA=∠EHD=90°,
∵在 Rt△EFA 中,∠DAE=30°,
∴AE=2EH=2x,
∴![]() ,
,
∵在 Rt△EHD 中,∠ADE=45°,
∴DH=EH=x,
∴![]() ,
,
∴![]() ,
,
∴x=1,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】盛盛同学到某高校游玩时,看到运动场的宣传栏中的部分信息(如下表):
院系篮球赛成绩公告 | |||
比赛场次 | 胜场 | 负场 | 积分 |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
盛盛同学结合学习的知识设计了如下问题,请你帮忙完成下列问题:
(1)从表中可以看出,负一场积______分,胜一场积_______分;
(2)某队在比完22场的前提下,胜场总积分能等于其负场总积分的2倍吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD之间的关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形?若存在,请写出来并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
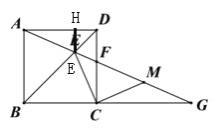
【题目】如图,点P是∠AOB的边OB上的一点.
(1)过点M画OB的平行线MN;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OB的垂线,交OA于点C:
则线段PH的长度是点P到 的距离, 是点C到直线OB的距离,因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 .(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts,
(1)当t=2s时,AB=24cm,此时,
①在直线l上画出A,B两点运动2s时的位置,并回答点A运动的速度是 cm/s,点B的运动速度是 cm/s;
②若点P为直线l上一点,且PA=OP+PB,求![]() 的值;
的值;
(2)在(1)的条件下,若A,B同时按原速度向左运动,再经过几秒,OA=3OB?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点 ![]() ,
, ![]() ,
, ![]() .下列说法正确的是( )
.下列说法正确的是( ) 
A.△ ![]() 与△ABC是位似图形,位似中心是点(1,0)
与△ABC是位似图形,位似中心是点(1,0)
B.△ ![]() 与△ABC是位似图形,位似中心是点(0,0)
与△ABC是位似图形,位似中心是点(0,0)
C.△ ![]() 与△ABC是相似图形,但不是位似图形
与△ABC是相似图形,但不是位似图形
D.△ ![]() 与△ABC不是相似图形
与△ABC不是相似图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为矩形ABCD的CD边延长线上一点,BE交AD于G , AF⊥BE于F , 图中相似三角形的对数是( ) 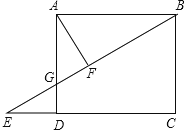
A.5
B.7
C.8
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com