
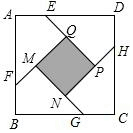
 如图,在边长为a(a>2)的正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,则正方形MNPQ的面积为2.
如图,在边长为a(a>2)的正方形各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,则正方形MNPQ的面积为2. 分析 根据图形可得4×(S△FSB+S四边形MFBG)=S正方形MNPQ+4×S四边形MFBG,即S正方形MNPQ=4S△FSB;由此即可解决问题.
解答 解:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图(2)).若将上述四个等腰三角形拼成一个新的正方形(无缝隙,不重叠),则新正方形的边长a;这个新正方形与原正方形ABCD的面积相等;
通过上述的分析,可以发现S正方形MNPQ=4•S△FSB=4$•\frac{1}{2}$×1×1=2.
故答案为2.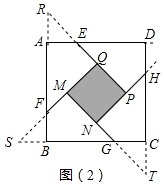
点评 主要考查了正方形的性质,等腰直角三角形的性质,等边三角形的性质以及全等三角形的性质的综合应用,解决问题的关键是作作辅助线构造直角三角形进行求解.通过本题我们可以体会到,运用等积变换的数学思想,不仅简化了几何计算,而且形象直观,易于理解,体现了数学的魅力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.767×1013 | B. | 6.767×1012 | C. | 67.67×1012 | D. | 6.767×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,∠BAC=90°,AB=6,AC=8.
如图,已知△ABC,∠BAC=90°,AB=6,AC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
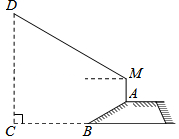 如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.
如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com