

 ,
,
 ,
, ,
,

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
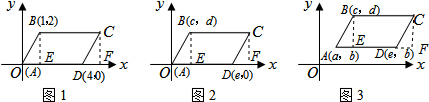
(1)在图1,2,3中,给出平行四边形![]() 的顶点
的顶点![]() 的坐标(如图所示),写出图1,2,3中的顶点
的坐标(如图所示),写出图1,2,3中的顶点![]() 的坐标,它们分别是
的坐标,它们分别是![]() , , ;
, , ;

(2)在图4中,给出平行四边形![]() 的顶点
的顶点![]() 的坐标(如图所示),求出顶点
的坐标(如图所示),求出顶点![]() 的坐标(
的坐标(![]() 点坐标用含
点坐标用含![]() 的代数式表示);
的代数式表示);

归纳与发现
(3)通过对图1,2,3,4的观察和顶点![]() 的坐标的探究,你会发现:无论平行四边
的坐标的探究,你会发现:无论平行四边
形![]() 处于直角坐标系中哪个位置,当其顶点坐标为
处于直角坐标系中哪个位置,当其顶点坐标为
![]() (如图4)时,则四个顶点的横坐标
(如图4)时,则四个顶点的横坐标![]() 之间的等量关系为 ;纵坐标
之间的等量关系为 ;纵坐标![]() 之间的等量关系为 (不必证明);
之间的等量关系为 (不必证明);
运用与推广
(4)在同一直角坐标系中有抛物线![]() 和三个点
和三个点
![]() ,
,![]() (其中
(其中![]() ).问当
).问当![]() 为何值时,该抛物线上存在点
为何值时,该抛物线上存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?并求出所有符合条件的
为顶点的四边形是平行四边形?并求出所有符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com