
【题目】已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°. 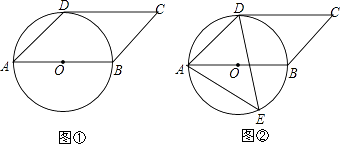
(1)如图①,判断CD与⊙O的位置关系,并说明理由;
(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.
【答案】
(1)解:(1)CD与圆O相切.
证明:如图①,连接OD,
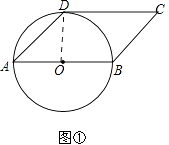
则∠AOD=2∠DAB=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠CDO=∠AOD=90°.
∴OD⊥CD.
∴CD与圆O相切.
(2)如图②,作EF⊥AB于F,连接BE,
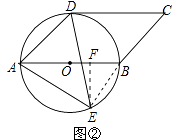
∵AB是圆O的直径,
∴∠AEB=90°,AB=2×3=6.
∵AE=5,
∴BE= ![]() =
= ![]() ,
,
∵sin∠BAE= ![]() .
.
∴ ![]() =
= ![]()
∴EF= ![]() .
.
【解析】(1)连接OD,则∠AOD为直角,由四边形ABCD是平行四边形,则AB∥DC.从而得出∠CDO=90°,即可证出答案.(2)作EF⊥AB于F,连接BE,根据圆周角定理得∠AEB=90°,然后根据勾股定理求得BE,然后根据sin∠BAE= ![]() 求得EF即可.
求得EF即可.
【考点精析】关于本题考查的勾股定理的概念和切线的判定定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
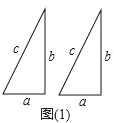
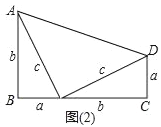
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
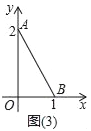
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…,Cn在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标:_____,写出一个满足条件的在y轴上的点坐标:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要将一批货物运往某地,打算租用某汽车运输公司的甲.乙两种货车,以前租用这两种货车的信息如下表所示;
第一次 | 第二次 | |
甲种货车辆数/辆 | 2 | 5 |
乙种货车辆数/辆 | 3 | 6 |
累计运货量/吨 | 15.5 | 35 |
现打算租用该公司4辆甲种货车和6辆乙种货车,可一次刚好运完这批货物.如果每吨运费为50元,该公司应付运费________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y= ![]() 与y=m﹣x的图象的一个交点是A(2,3),其中k、m为常数.
与y=m﹣x的图象的一个交点是A(2,3),其中k、m为常数.
(1)求k、m的值,画出函数的草图.
(2)根据图象,确定自变量x的取值范围,使一次函数的函数值大于反比例函数的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,2016排列成如图所示的形式.

(1)用一个矩形随意框住4个数,把其中最小的数记为![]() ,另三个数用含
,另三个数用含![]() 式子表示出来,当被框住的4个数之和等于418时,
式子表示出来,当被框住的4个数之和等于418时,![]() 值是多少?
值是多少?
(2)被框住的4个数之和能否等于724?如果能,请求出此时x值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两同学用两枚质地均匀的骰子作游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局. 根据上述规则,解答下列问题;
(1)随机掷两枚骰子一次,用列表法求点数和为8的概率;
(2)甲先随机掷两枚骰子一次,点数和是7,求乙随机掷两枚骰子一次获胜的概率. (骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com