
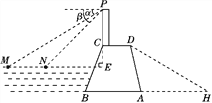
【题目】某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米).
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1∶0.25.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1∶1.75.施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备.工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan 31°≈0.60,sin 31°≈0.52)
【答案】(1)两渔船M,N之间的距离约为20米;(2)施工队原计划平均每天填筑土石方864立方米.
【解析】试题分析:(1)在直角△PEN,利用三角函数即可求得ME的长,根据MN=EM﹣EN求解;
(2)过点D作DN⊥AH于点N,利用三角函数求得AN和AH的长,进而求得△ADH的面积,得到需要填筑的土石方数,再根据结果比原计划提前20天完成,列方程求解.
试题解析:(1)由题意得∠E=90°,∠PME=α=31°,∠PNE=β=45°,PE=30米.
在Rt△PEN中,PE=NE=30米,
在Rt△PEM中,tan 31°=![]() ,∴ME≈
,∴ME≈![]() =50(米).
=50(米).
∴MN=EM-EN≈50-30=20(米).
答:两渔船M,N之间的距离约为20米.
(2)如图,过点D作DG⊥AB于G,坝高DG=24米.
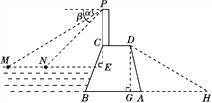
∵背水坡AD的坡度i=1∶0.25,∴DG∶AG=1∶0.25,
∴AG=24×0.25=6(米).
∵背水坡DH的坡度i=1∶1.75,
∴DG∶GH=1∶1.75,∴GH=24×1.75=42(米).
∴AH=GH-GA=42-6=36(米).
∴S△ADH=![]() AH·DG=
AH·DG=![]() ×36×24=432(平方米).
×36×24=432(平方米).
∴需要填筑的土石方为432×100=43 200(立方米).
设施工队原计划平均每天填筑土石方x立方米,
根据题意,得10+![]() =
=![]() -20.
-20.
解方程,得x=864.
经检验:x=864是原方程的根且符合题意.
答:施工队原计划平均每天填筑土石方864立方米.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
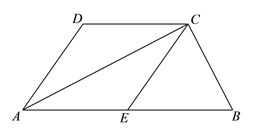
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果为F(n)=3n+1;②当n为偶数时,结果为F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
![]()
若n=24,则第100次“F”运算的结果是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C在数轴上表示的数是10,若线段 AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的数度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 ;(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式 BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为提高学生的身体素质,经常在课间开展学生跳绳比赛,下表为该校七年级![]() 班
班![]() 名学生参加某次跳绳比赛的情况,规定标准数量为每人每分钟
名学生参加某次跳绳比赛的情况,规定标准数量为每人每分钟![]() 个.
个.
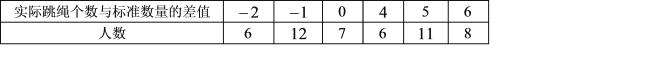
(1)求七年级![]() 班
班![]() 人中跳绳最多的同学一分钟跳的次数是多少个,跳绳最少的同学一分钟跳的次数是多少个?
人中跳绳最多的同学一分钟跳的次数是多少个,跳绳最少的同学一分钟跳的次数是多少个?
(2)跳绳比赛的计分方式如下:
①若每分钟跳绳个数是规定标准数量,不计分;
②若每分钟跳绳个数超过规定标准数量,每多跳![]() 个绳加
个绳加![]() 分
分
③若每分钟跳绳个数没有达到规定标准数量,每少跳![]() 个绳扣
个绳扣![]() 分
分
如果班级跳绳总积分超过![]() 分,便可得到学校的奖励,请你通过计算说明七年级
分,便可得到学校的奖励,请你通过计算说明七年级![]() 班能否得到学校奖励?
班能否得到学校奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是![]() ,则点C的坐标是( )
,则点C的坐标是( )

A. (4,2) B. (2,4) C. (![]() ,3) D. (3,
,3) D. (3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学探究活动中:如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,
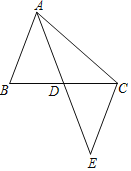
求AD的取值范围.小明给出了一种方法,步骤如下:
①过点C作一条与AB平行的线;
②延长AD交这条平行线于点E;
③通过证明得到AD=DE,AB=CE;
④利用△ACE三边的数量关系得到AD的取值范围.
根据这个方法,请你完成下面两个问题:
(1)求证:AD=DE,AB=CE;
(2)求AD的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com