Question

3．如图所示，CD为⊙O的直径，AD、AB、BC分别与⊙O相切于点D、E、C（AD＜BC）．连接DE并延长与直线BC相交于点P，连接OB．
（1）求证：BC=BP；
（2）若DE•OB=40，求AD•BC的值；
（3）在（2）条件下，若S_△ADE：S_△PBE=16：25，求四边形ABCD的面积．

Answer 1

分析 （1）由于点O是CD的中点，所以要证BC=BP，只要证明OB∥DP即可；
（2）由DE•OB=40可以想到比例式，由题意可以证明△DEC∽△OCB，由此得DE•OB=OC•DC=40，则OC=2$\sqrt{5}$，再证△ADO∽△OCB即可；
（3）易证△ADE∽△BPE，根据面积的比等于相似比的平方得$\frac{S△ADE}{S△PBE}$=$\frac{A{D}^{2}}{B{P}^{2}}$=$\frac{16}{25}$，则BC=5，又四边形ABCD是梯形，按其面积公式即可求解．

解答 解：（1）证明：连接OE，如下图①，
∵BC、AB分别与⊙O相切于点C、E，
∴∠OCB=∠OEB=90°，
在Rt△OCB与Rt△OEB中，
    $\left\{\begin{array}{l}{OC=OE（同圆的半径相等）}\\{OB=OB（公共边相等）}\end{array}\right.$
Rt△OCB≌Rt△OEB（HL）
∴∠COB=∠EOB
∵同弧所对的圆周角是其所对的圆心角的一半，
∴∠COB=$\frac{1}{2}$∠COE=∠CDP，
∴DP∥OB，
又点O是CD的中点，
∴OB是△CDP的中位线，
∴BC=BP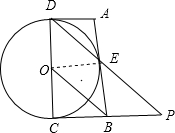
  
                         图①
（2）连接OA、OE、CE，如下图②所示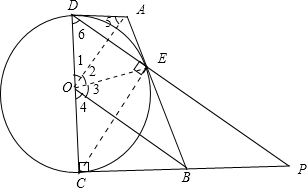
图②
∵CD是⊙O的直径，
∴∠DEC=90°，
又BC与⊙O相切于点C，
∴∠DEC=∠OCB=90°，
又∠4=∠6
∴△DEC∽△OCB，
∴$\frac{DE}{OC}=\frac{DC}{OB}$
∴DE•OB=OC•DC=40
∴DC=2OC
OC²=20，OC=2$\sqrt{5}$，
∵又∠1=∠2，∠3=∠4，
∴∠1+∠4=90°，
又∠1+∠5=90°，
∴∠4=∠5
∴△ADO∽△OCB
∴$\frac{AD}{OC}=\frac{OD}{BC}$
∴AD•BC=OC•OD=OC²=20
即：AD•BC=20
（3）∵AD、BC分别与⊙O相切于点D、C，如图②所示，
∴CD⊥AD，CD⊥PC，
∴AD∥PB
∴△ADE∽△BPE
∴$\frac{S△ADE}{S△PBE}$=$\frac{A{D}^{2}}{B{P}^{2}}$=$\frac{16}{25}$，
∴$\frac{AD}{BC}=\frac{AD}{BP}=\frac{4}{5}$，
       即：AD=$\frac{4}{5}$BC=$\frac{4}{5}$BP
      又∵AD•BC=20
∴BC²=25
    即：BC=5
∴S四边形ABCD=$\frac{1}{2}$（AD+BC）•2OC
=OC（AD+BP）
=2$\sqrt{5}$•$\frac{9}{5}$BC
=2$\sqrt{5}$×$\frac{9}{5}$×5
=18$\sqrt{5}$
即：四边形ABCD的面积为18$\sqrt{5}$

点评 本题考查了圆的切线的性质、相似的性质与判定等知识点，本题的难点是相似的判定与性质的应用，这也是解（2）、（3）两个小题的关键．