【题目】下列说法正确的是（ ）
A.了解一批灯泡的使用寿命采用全面调查
B.一组数据6，5，3，5，4的众数是5，中位数是3
C.“367人中必有2人的生日是同一天”是必然事件
D.一组数据10，11，12，9，8的平均数是10，方差是1.5
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
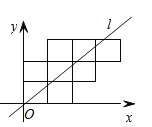
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线
将这八个正方形分成面积相等的两部分，则该直线的解析式为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019新型冠状病毒，因武汉病毒性肺炎病例而被发现，2020年1月12日被世界卫生组织命名“2019-nCoV”．冠状病毒是一个大型病毒家族，借助电子显微镜，我们可以看到这些病毒直径约为125纳米（1纳米=1 
10-9米），125纳米用科学记数法表示等于（ ）米
A.1.2510-10B.1.2510-11C.1.25 10-8D.1.2510-7
查看答案和解析>>
科目：初中数学 来源： 题型：
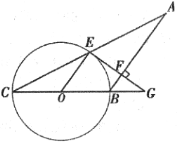
【题目】如图，在△ABC中，AB=BC，以BC为直径作⊙ O交AC于点E，过点E作AB的垂线交AB于点F，交CB的延长线于点G．
（1）求证：EG是⊙O的切线；
（2）若BG=OB，AC=6，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销
件．已知产销两种产品的有关信息如下表：
产品 | 每件售价（万元） | 每件成本（万元） | 每年其他费用（万元） | 每年最大产销量（件） |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中
为常数，且
．
（1）若产销甲、乙两种产品的年利润分别为
万元、
万元，直接写出、与的函数关系式（写出自变量的取值范围）；
（2）分别求出产销两种产品的最大年利润；
（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据完全平方公式可以作如下推导（a、b都为非负数）
∵ a-2
+b=(
-
)2≥0 ∴ a-2+b≥0
∴ a+b≥2 ∴ 
≥
其实，这个不等关系可以推广，
≥
… …
（以上an都是非负数）
我们把这种关系称为：算术—几何均值不等式
例如：x为非负数时，
，则
有最小值．
再如：x为非负数时，x+x+
．
我们来研究函数：
（1）这个函数的自变量x的取值范围是 ；
（2）完成表格并在坐标系中画出这个函数的大致图象；
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
（3）根据算术—几何均值不等式，该函数在第一象限有最 值，是 ；
（4）某同学在研究这个函数时提出这样一个结论：当x>a时，y随x增大而增大,则a的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校七年级共有500名学生，为了解该年级学生的课外阅读情况，将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本，根据数据绘制了如下的表格和统计图：
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
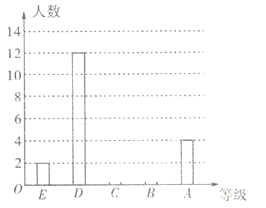
根据上面提供的信息，回答下列问题：
(1)统计表中的
，
；并补全条形统计图；
(2)根据抽样调查结果，请估计该校七年级学生一学期的阅读量为“
等”的有多少人?
(3)样本中阅读量为“等”的4名学生中有2名男生和2名女生，现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
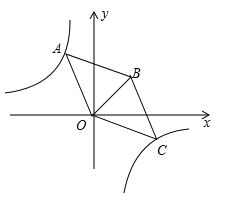
【题目】如图，在平面直角坐标系中，菱形
的顶点
为坐标原点，且与反比例函数
的图象相交于
，
两点，且点的纵坐标为
，已知点
，则
的值为（ ）．
A.
B.
C.9D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
