练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．若x1，x2，x3，x4，x5满足方程组：$\left\{\begin{array}{l}2{x_1}+{x_2}+{x_3}+{x_4}+{x_5}=6\\{x_1}+2{x_2}+{x_3}+{x_4}+{x_5}=12\\{x_1}+{x_2}+2{x_3}+{x_4}+{x_5}=24\\{x_1}+{x_2}+{x_3}+2{x_4}+{x_5}=48\\{x_1}+{x_2}+{x_3}+{x_4}+2{x_5}=96\end{array}\right.$；则3x4+2x5的值是181．

    分析 本题的方程组为对称轮换式，把5个方程相加得x1+x2+x3+x4+x5=31，要求x4、x5，就分别与④⑤相减即可．

    解答 解：①+②+③+④+⑤得6x1+6x2+6x3+6x4+6x5=186
    解得x1+x2+x3+x4+x5=31 ⑥
    ④-⑥得：x4=17，
    ⑤-⑥得：x5=65，
    ∴3x4+2x5=3×17+2×65=181．
    故答案为：181．

    点评 本题考查了代数式的求值，代数式中涉及的字母为方程组的未知数，虽然方程组比较复杂，但有一定的规律，需要观察规律求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．计算：-3+4的结果等于（　　）
    A．7B．-7C．1D．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

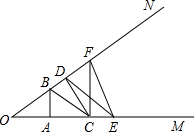    4．如图，∠MON两边上分别有A，C，E及D，F，B六个点，且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1，则S△CDF=$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．观察一列数2，4，8，16，32，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是2；根据此规律，如果an（n为正整数）表示这个数列的第n项，那么a18=218，an=2n；
    （2）如果欲求1+3+32+33+…+320的值，可令S=1+3+32+33+…+320…①
    将①式两边同乘以3，得3S=3+32+33+34+…+321…②
    由②减去①式，得S=$\frac{{3}^{21}-1}{2}$．
    （3）用由特殊到一般的方法知：若数列a1，a2，a3，…，an，从第二项开始每一项与前一项之比的常数为q，则an=${{a}_{1}q}^{n-1}$（用含a1，q，n的代数式表示），如果这个常数q≠1，那么Sn=a1+a2+a3+…+an=$\frac{{a}_{1}{（q}^{n}-1）}{q-1}$．（用含a1，q，n的代数式表示）．
    （4）已知数列满足（3），且a6-a4=24，a3a5=64，求S8=a1+a2+a3+…+a8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．化简$\frac{{\sqrt{2}+\sqrt{5}-\sqrt{3}}}{{2\sqrt{30}-6\sqrt{2}+4\sqrt{3}}}$的结果是（　　）
    A．$2\sqrt{6}$B．$\frac{{\sqrt{6}}}{2}$C．$\frac{{\sqrt{6}}}{6}$D．$\frac{{\sqrt{6}}}{12}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．某校八年级五班有7个合作学习小组，各学习小组的人数分别为：5，5，6，x，7，7，6，已知这组数据的平均数是6，则这组数据的众数和中位数分别是（　　）
    A．7，6B．6，6C．5，5D．7，7

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若式子$\sqrt{x-2}$在实数范围内有意义，则x的取值范围是（　　）
    A．x＞2B．x≥2C．x≠2D．x≥0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．若关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-1-a}\\{x-2y=3}\end{array}\right.$的解满足x+y＞-2，则a的取值范围是（　　）
    A．a＜-2B．a＞2C．a＜2D．a＞-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列调查，适合用全面调查的是（　　）
    A．了解一批炮弹的杀伤半径
    B．了解某电视台《我是大明星》栏目的收视率
    C．对市场上某种酒质量情况的调查
    D．调查一架隐形战机的各零部件的质量

    查看答案和解析>>

    同步练习册答案