
分析 (1)根据方程的系数结合根的判别式,即可得出△=-8m+4≥0,解之即可得出m的取值范围;
(2)根据根与系数的关系可得x1+x2=2(m-1)、x1•x2=m2,结合x1•x2+x1+x2=1即可得出关于m的一元二次方程,解之即可得出结论.
解答 解:(1)∵关于x的方程x2-2(m-1)x+m2=0有两个实数根,
∴△=[-2(m-1)]2-4×1×m2=-8m+4≥0,
解得:m≤$\frac{1}{2}$.
(2)∵关于x的方程x2-2(m-1)x+m2=0有两个实数根x1、x2,
∴x1+x2=2(m-1),x1•x2=m2,
∴x1•x2+x1+x2=m2+2(m-1)=1,即m2+2m-3=0,
解得:m=-3或m=1(舍去).
点评 本题考查了根与系数的关系、根的判别式以及解一元二次方程,解题的关键是:(1)牢记“当△≥0时,方程有两个实数根”;(2)根据根与系数的关系结合x1•x2+x1+x2=1找出关于m的一元二次方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
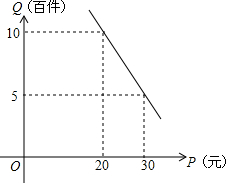 在精准对口扶贫活动中,甲单位将经营状况良好的某种专卖店以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的乙户,并约定从该店经营的利润中,首先保证乙户的一家人每月最低生活费的开支3600元后,逐步偿还转让费(不计利息).从甲单位提供的相关资料中可知这种消费品的进价是每件14元;月销售量Q(百件)与销售单价P(元)的关系如图所示;维持的正常运转每月需工资外的各种开支2000元.
在精准对口扶贫活动中,甲单位将经营状况良好的某种专卖店以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的乙户,并约定从该店经营的利润中,首先保证乙户的一家人每月最低生活费的开支3600元后,逐步偿还转让费(不计利息).从甲单位提供的相关资料中可知这种消费品的进价是每件14元;月销售量Q(百件)与销售单价P(元)的关系如图所示;维持的正常运转每月需工资外的各种开支2000元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
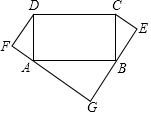 如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
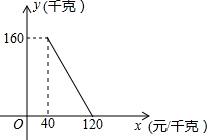 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
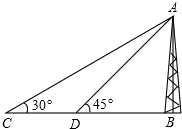 如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )
如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )| A. | 50$\sqrt{3}$米 | B. | 100$\sqrt{3}$米 | C. | 50($\sqrt{3}$+1)米 | D. | 50($\sqrt{3}$-1)米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com