
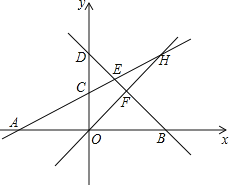
【题目】如图,直线AC:y=![]() x+2分别交x轴和y轴于A,C两点,直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,直线AC与BD交于点E,且OA=OB.
x+2分别交x轴和y轴于A,C两点,直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,直线AC与BD交于点E,且OA=OB.
(1)求直线BD的解析式和E的坐标.
(2)若直线y=x分别与直线AC,BD交于点H和F,求四边形ECOF的面积.
【答案】(1)y=﹣x+4,点E坐标为(![]() ,
,![]() );(2)
);(2)![]() .
.
【解析】
(1)先求直线AC:y=![]() x+2与x轴和y轴的交点A,C,由OA=OB得点坐标,代入直线BD:y=-x+b,求出b,即可知直线BD的解析式;再把直线BD的解析式与直线AC:y=
x+2与x轴和y轴的交点A,C,由OA=OB得点坐标,代入直线BD:y=-x+b,求出b,即可知直线BD的解析式;再把直线BD的解析式与直线AC:y=![]() x+2联立即可求出点E的坐标.
x+2联立即可求出点E的坐标.
(2)由(1)知点C,D,E的坐标,再联立y=x和直线BD的解析式,求出点F的坐标,由三角形DOF的面积减去三角形DCE的面积,即可求出四边形ECOF的面积.
解:(1)∵直线AC:y=![]() x+2分别交x轴和y轴于A,C两点,
x+2分别交x轴和y轴于A,C两点,
∴A(﹣4,0),C(0,2),
∵OA=OB,
∴OA=OB=4,B(4,0),
∵直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,
∴0=﹣4+b,
∴b=4,D(0,4)
∴直线BD:y=﹣x+4.
解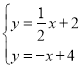 得
得 ![]()
∴![]()
综上,直线 直线BD的解析式为:y=﹣x+4,点E坐标为![]() .
.
(2)由(1)知:C(0,2),D(0,4),E![]() ,
,
且由![]() ,得点F(2,2),
,得点F(2,2),
∴S四边形ECOF=S△DOF﹣S△DCE
=4×2÷2﹣(4﹣2)×![]() ÷2
÷2
=4﹣![]()
=![]()
故四边形ECOF的面积为![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:
![]()
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: ,B: ;
(2)观察数轴,与点A的距离为4的点表示的数是: ;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数 表示的点重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距240千米的A,B两地同时相向匀速出发,甲车出发0.5小时后发现有东西落在出发地A地,于是立即按原速沿原路返回,在A地取到东西后立即以原速继续向B地行驶,并在途中与乙车第一次相遇,相遇后甲、乙两车继续以各自的速度朝着各自的方向匀速行驶,当乙车到达A地后,立即掉头以原速开往B地(甲车取东西、掉头和乙车掉头的时间均忽略不计).两车之间的距离y(千米)与甲车出发的时间x(小时)之间的部分关系如图所示,则当乙车到达B地时,甲车与B地的距离为_____千米.
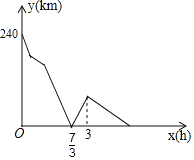
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向而行.已知甲车速度为
两地同时出发,相向而行.已知甲车速度为![]() ,乙车速度为
,乙车速度为![]() ,经过
,经过![]() 后两车相距
后两车相距![]() ,则
,则![]() 的值是( )
的值是( )
A.2B.10C.2或10D.2或2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=2,BC=1.5,矩形在直线上绕其右下角的顶点B向右第一次旋转90°至图①位置,再绕右下角的顶点继续向右第二次旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段引导市民节约用水。某市规定如下用水收费标准:每月每户的用水不超过6![]() 时,水费按正常收费;超过6
时,水费按正常收费;超过6![]() 时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9
时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9![]() ,缴纳水费为27元;3月份的用水量为11
,缴纳水费为27元;3月份的用水量为11![]() ,缴纳水费为37元。
,缴纳水费为37元。
(1)求在限定量以内每吨多少元?超出部分的水费每吨多少元?
(2)若该市某居民今年4月份的用水量为13![]() . 则应缴纳水费多少元?
. 则应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1=![]() ,
,
第2个等式:a2=![]() ,
,
第3个等式:a3=![]() ,
,
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+…+a2019的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com