
【题目】如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)

解:垂直.理由如下:
∵DE⊥AC,AC⊥BC,
∴∠AED=∠ACB=90°( 垂直的意义 ).
∴DE∥BC( ① )
∴∠1=∠DCB( ② )
∵∠1与∠2互补(已知).
∴∠DCB与∠2互补
∴ ③ (同旁内角互补,两直线平行)
∴∠BFH=∠CDB( ④ )
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFH= ⑤ ( ⑥ ).
∴HF⊥AB.
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从友谊体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同、每个篮球的价格相同),若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需要从该体育用品商店一次性购买足球和篮球共20个.要求购买篮球数不少于足球数的2倍,总费用不超过1840元,那么这所中学有哪几种购买方案?哪种方案所需费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
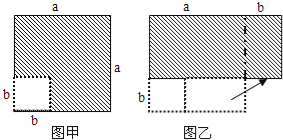
A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个正方形边长分别为a、b.
(1)求阴影部分的面积.
(2)如果a+b=17,ab=60,求阴影部分的面积.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/17/1904284875390976/1906414662729728/STEM/433f25b861984b60a78ae031a98667fa.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有5个质地、大小完全相同的小球上分别标有数字-1,-2,1,2,3.先将标有数字-2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现分别从两个盒子里各随即取出一个小球.
(1)请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果;
(2)求取出的两个小球上的数字之和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
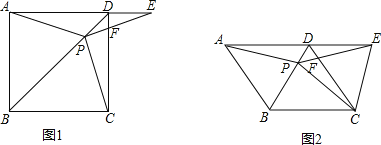
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.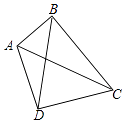
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: ![]() .
.
(3)①若AB=BC=4,AD+DC=6,求 ![]() 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com