
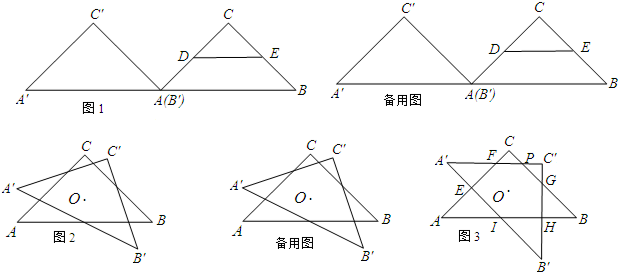
 如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.分析 (1)由DE∥BC得到∠BCD=∠CDE=30°,再由∠ACB=120°,得到∠ACD=120°-30°=90°,则△ACD是直角三角形.
(2)分类讨论:当∠CDE=∠ECD时,EC=DE;当∠ECD=∠CED时,CD=DE;当∠CED=∠CDE时,EC=CD;然后利用等腰三角形的性质和三角形的内角和定理进行计算.
解答 解:(1)∵△ABC中,AC=BC,
∴∠A=∠B=$\frac{180°-∠ACB}{2}$=$\frac{180°-120°}{2}$=30°,
∵DE∥BC,
∴∠ADE=∠B=30°,
又∵∠CDE=30°,
∴∠ADC=∠ADE+∠CDE=30°+30°=60°,
∴∠ACD=180°-∠A-∠ADC=180°-30°-60°=90°,
∴△ACD是直角三角形;
(2)△ECD可以是等腰三角形.理由如下:
①当∠CDE=∠ECD时,EC=DE,
∴∠ECD=∠CDE=30°,
∵∠AED=∠ECD+∠CDE,
∴∠AED=60°,
②当∠ECD=∠CED时,CD=DE,
∵∠ECD+∠CED+∠CDE=180°,
∴∠CED=$\frac{180°-∠CDE}{2}$=$\frac{180°-30°}{2}$=75°,
∴∠AED=180°-∠CED=105°,
③当∠CED=∠CDE时,EC=CD,
∠ACD=180°-∠CED-∠CDE=180°-30°-30°=120°,
∵∠ACB=120°,
∴此时,点D与点B重合,不合题意.
综上,△ECD可以是等腰三角形,此时∠AED的度数为60°或105
点评 本题考查了三角形内角和定理:三角形内角和为180°.也考查了分类讨论思想的运用以及等腰三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | 在367人中至少有两个人的生日相同 | |
| B. | 一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 一个不透明的袋中装有3个红球,5个白球,搅匀后想从中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 160元 | B. | 180元 | C. | 200元 | D. | 220元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小文家的小区有一人工湖,湖的北岸有一条笔直的小路,湖上原有一座小桥与小路垂直相通,现小桥有一部分已断裂,另一部分完好.小文站在完好的桥头点A处,测得北岸路边的小树所在位置D点在他的北偏西30°,向正北方向前进32米到断口B点,又测得D点在他的北偏西45°.请根据小文的测量数据,计算小桥断裂部分的长.($\sqrt{3}≈1.73$,结果保留整数)
如图,小文家的小区有一人工湖,湖的北岸有一条笔直的小路,湖上原有一座小桥与小路垂直相通,现小桥有一部分已断裂,另一部分完好.小文站在完好的桥头点A处,测得北岸路边的小树所在位置D点在他的北偏西30°,向正北方向前进32米到断口B点,又测得D点在他的北偏西45°.请根据小文的测量数据,计算小桥断裂部分的长.($\sqrt{3}≈1.73$,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每人销售台数 | 20 | 17 | 13 | 8 | 5 | 4 |
| 人数 | 1 | 1 | 2 | 5 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到四边形AMEF,EM交线段DC于点G,EM的延长线交线段BC于点P,连接AP、AG.
如图,将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°),得到四边形AMEF,EM交线段DC于点G,EM的延长线交线段BC于点P,连接AP、AG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com