
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.

(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
【答案】(1)60°;(2)若直线EF平分∠BOD,t的值为12s或36s.
【解析】试题分析:(1)根据角平分线的性质,可得∠AOC的值,再根据互为补角和互为余角的性质,求出∠BOD的值;
(2)①根据题意,分为OE平分∠AOB和OF平分∠AOB两种情况讨论求解;
②根据题意,分两种情况:当OE平分∠BOD和OF平分∠BOD时,进行画图求解.
试题解析:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,

即9t+30°﹣3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,
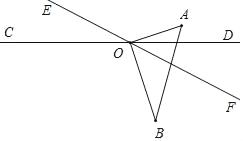
即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=![]() ∠BOD,
∠BOD,

即9t﹣60°﹣3t=![]() (60°﹣3t),
(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=![]() ∠BOD,
∠BOD,
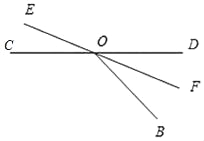
即3t﹣(9t﹣240°)=![]() (3t﹣60°),
(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C

证明:∵BD⊥AC,EF⊥AC
∴∠2=∠3=90°
∴BD∥EF ( )
∴∠4=_____ ( )
∵∠1=∠4
∴∠1=_____
∴DG∥BC ( )
∴∠ADG=∠C( )
查看答案和解析>>
科目:初中数学 来源: 题型:
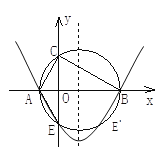
【题目】如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2= 17, 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
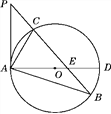
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;(2)求证:CD是⊙P的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接到一批服装加工业务,若由甲车间独做,可比规定时间提前8天完成,甲车间在制作完这批服装的60%后因另有任务,立即将剩余服装全部交给乙车间,结果刚好按规定时间完成.已知甲、乙两个车间每天分别制作200和120件服装,求该工厂所接的这批服装的件数和规定时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
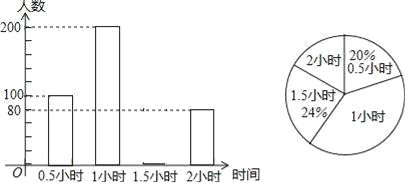
(1)求被抽样调查的学生有多少人?并补全条形统计图;
(2)该校共有1850名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com