
”¾ĢāÄæ”æŌŚĮ½Ē§¶ąÄźĒ°ĪŅ¹ś¹ÅĖćŹõÉĻ¼ĒŌŲÓŠ”°¹“Čż¹ÉĖÄĻŅĪå”±.ÄćÖŖµĄĖüµÄŅāĖ¼Āš£æ
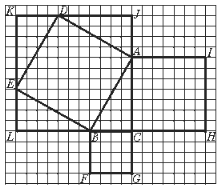
ĖüµÄŅāĖ¼ŹĒĖµ£ŗČē¹ūŅ»øöÖ±½ĒČż½ĒŠĪµÄĮ½ĢõÖ±½Ē±ß³¤·Ö±šĪŖ3ŗĶ4øö³¤¶Čµ„Ī»£¬ÄĒĆ“ĖüµÄŠ±±ßµÄ³¤Ņ»¶ØŹĒ5øö³¤¶Čµ„Ī»£¬¶ųĒŅ3”¢4”¢5ÕāČżøöŹżÓŠÕāŃłµÄ¹ŲĻµ£ŗ32+42=52.
£Ø1£©ĒėÄć¶Æ¶ÆÄŌ½ī£¬ÄÜ·ńŃéÖ¤ÕāøöŹĀŹµÄŲ£æøĆČēŗĪæ¼ĀĒÄŲ£æ
£Ø2£©ĒėÄć¹Ū²ģĻĀĮŠĶ¼ŠĪ£¬Ö±½ĒČż½ĒŠĪABCµÄĮ½ĢõÖ±½Ē±ßµÄ³¤·Ö±šĪŖAC=7£¬BC=4£¬ĒėÄćŃŠ¾æÕāøöÖ±½ĒČż½ĒŠĪµÄŠ±±ßABµÄ³¤µÄĘ½·½ŹĒ·ńµČÓŚ42+72£æ
”¾“š°ø”æ¼ū½āĪö
”¾½āĪö”æ
£Ø1£©±ß³¤µÄĘ½·½¼“ŅŌ“Ė±ß³¤ĪŖ±ßµÄÕż·½ŠĪµÄĆ껿£¬¹ŹæÉĶعżĆ껿ŃéÖ¤£®·Ö±šŅŌÕāøöÖ±½ĒČż½ĒŠĪµÄČż±ßĪŖ±ßĻņĶā×öÕż·½ŠĪ£¬Ēó³öČżøöÕż·½ŠĪµÄĆ껿£¬¼“æÉÖ¤Ć÷£»
£Ø2£©¹Ų¼üŹĒ¼ĘĖćSÕż·½ŠĪABED=SÕż·½ŠĪKLCJ©4SRt”÷ABC£¬ŌŁ¼ÓŅŌŃéÖ¤¼“æÉ£®
£Ø1£©±ß³¤µÄĘ½·½¼“ŅŌ“Ė±ß³¤ĪŖ±ßµÄÕż·½ŠĪµÄĆ껿£¬¹ŹæÉĶعżĆ껿ŃéÖ¤£®·Ö±šŅŌÕāøöÖ±½ĒČż½ĒŠĪµÄČż±ßĪŖ±ßĻņĶā×÷Õż·½ŠĪ£¬ČēĶ¼£ŗAC=4£¬BC=3£¬

SÕż·½ŠĪABED=SÕż·½ŠĪFCGH©4SRt”÷ABC
=£Ø3+4£©2©4”Į![]() ”Į3”Į4
”Į3”Į4
=72©24
=25£¬
¼“AB2=25£¬
ÓÖ”ßAC=4£¬BC=3£¬
AC2+BC2=42+32=25
”ąAB2=AC2+BC2£®
£Ø2£©ČēĶ¼

SÕż·½ŠĪABED=SÕż·½ŠĪKLCJ©4SRt”÷ABC=£Ø4+7£©2©4”Į![]() ”Į4”Į7=121©56=65=42+72£®
”Į4”Į7=121©56=65=42+72£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻB£½90”ć£¬AB£½7 cm£¬AC£½25 cm.µćP“ÓµćAŃŲAB·½ĻņŅŌ1 cm/sµÄĖŁ¶ČŌĖ¶ÆÖĮµćB£¬µćQ“ÓµćBŃŲBC·½ĻņŅŌ6 cm/sµÄĖŁ¶ČŌĖ¶ÆÖĮµćC£¬P£¬QĮ½µćĶ¬Ź±³ö·¢£®
(1)ĒóBCµÄ³¤£»
(2)µ±µćP£¬QŌĖ¶Æ2 sŹ±£¬ĒóP£¬QĮ½µćÖ®¼äµÄ¾ąĄė£»
(3)P£¬QĮ½µćŌĖ¶Æ¼øĆėŹ±£¬AP£½CQ?

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潚ĒļŹ®ŌĀ£¬³¤É³ŹŠÄ³ÖŠŃ§×éÖÆĘßÄź¼¶Ń§ÉśČ„ij×ŪŗĻŹµ¼ł»łµŲ½ųŠŠĒļ¼¾Éē»įŹµ¼ł»ī¶Æ£¬ĆæČĖŠč¹ŗĀņŅ»ÕÅĆÅʱ£¬øĆ×ŪŗĻŹµ¼ł»łµŲµÄĆÅʱ¼ŪøńĪŖĆæÕÅ240ŌŖ£¬Čē¹ūŅ»“Ī¹ŗĀņ500ÕÅŅŌÉĻ£Ø²»ŗ¬500ÕÅ£©ĆÅʱ£¬ŌņĆÅʱ¼ŪøńĪŖĆæÕÅ220ŌŖ£¬Ēė»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĮŠŹ½±ķŹ¾nøöČĖ²Ī¼ÓĒļ¼¾Éē»įŹµ¼ł»ī¶ÆĖłŠčĒ®Źż£»
£Ø2£©Ä³Š£ÓĆ132000ŌŖæÉŅŌ¹ŗĀņ¶ąÉŁÕÅĆÅʱ£»
£Ø3£©Čē¹ūĪŅŠ£490ČĖ²Ī¼ÓĒļ¼¾Éē»įŹµ¼ł£¬ŌõŃł¹ŗĀņĆÅʱ»ØĒ®×īÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æA”¢B”¢C ĪŖŹżÖįÉĻČżµć£¬Čōµć C µ½µć A µÄ¾ąĄėŹĒµć C µ½µć B µÄ¾ąĄėµÄ 2±¶£¬Ōņ³Ęµć C ŹĒ£ØA£¬B£©µÄĘęŅģµć£¬ĄżČēĶ¼ 1 ÖŠ£¬µć A ±ķŹ¾µÄŹżĪŖ©1£¬µćB ±ķŹ¾µÄŹżĪŖ 2£¬±ķŹ¾ 1 µÄµć C µ½µć A µÄ¾ąĄėĪŖ 2£¬µ½µć B µÄ¾ąĄėĪŖ 1£¬ŌņµćC ŹĒ£ØA£¬B£©µÄĘęŅģµć£¬µ«²»ŹĒ£ØB£¬A£©µÄĘęŅģµć£®
(1)ŌŚĶ¼ 1 ÖŠ£¬Ö±½ÓĖµ³öµć D ŹĒ£ØA£¬B£©»¹ŹĒ£ØB£¬C£©µÄĘęŅģµć£»
(2)ČēĶ¼ 2£¬ČōŹżÖįÉĻ M”¢N Į½µć±ķŹ¾µÄŹż·Ö±šĪŖ©2 ŗĶ 4£¬£ØM£¬N£©µÄĘęŅģµć K ŌŚ M”¢N Į½µćÖ®¼ä£¬ĒėĒó³ö K µć±ķŹ¾µÄŹż£»
(3)ČēĶ¼ 3£¬A”¢B ŌŚŹżÖįÉĻ±ķŹ¾µÄŹż·Ö±šĪŖ©20 ŗĶ 40£¬ĻÖÓŠŅ»µć P “Óµć B ³ö·¢£¬Ļņ×óŌĖ¶Æ£®
¢ŁČōµć P µ½“ļµć A Ķ£Ö¹£¬Ōņµ±µć P ±ķŹ¾µÄŹżĪŖ¶ąÉŁŹ±£¬P”¢A”¢B ÖŠĒ”ÓŠŅ»øöµćĪŖĘäÓąĮ½µćµÄĘęŅģµć£æ
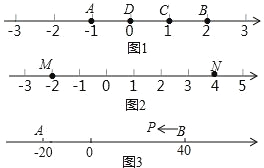
¢ŚČōµć P µ½“ļµć A ŗó¼ĢŠųĻņ×óŌĖ¶Æ£¬ŹĒ·ń“ęŌŚŹ¹µĆ P”¢A”¢B ÖŠĒ”ÓŠŅ»øöµćĪŖĘäÓąĮ½µćµÄĘęŅģµćµÄĒéæö£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³ö“ĖŹ± PB µÄ¾ąĄė£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy= ![]() x2+bx+cÓėxÖį½»ÓŚA£Ø5£¬0£©”¢B£Ø©1£¬0£©Į½µć£¬¹żµćA×÷Ö±ĻßAC”ĶxÖį£¬½»Ö±Ļßy=2xÓŚµćC£»
x2+bx+cÓėxÖį½»ÓŚA£Ø5£¬0£©”¢B£Ø©1£¬0£©Į½µć£¬¹żµćA×÷Ö±ĻßAC”ĶxÖį£¬½»Ö±Ļßy=2xÓŚµćC£»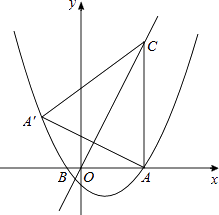
£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ĒóµćA¹ŲÓŚÖ±Ļßy=2xµÄ¶Ō³ĘµćA”äµÄ×ų±ź£¬ÅŠ¶ØµćA”äŹĒ·ńŌŚÅ×ĪļĻßÉĻ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©µćPŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻߣ¬½»Ļ߶ĪCA”äÓŚµćM£¬ŹĒ·ń“ęŌŚÕāŃłµÄµćP£¬Ź¹ĖıߊĪPACMŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
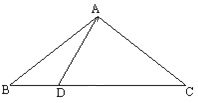
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬”÷ABCÖŠ£¬AB=AC=10£¬BC=16£¬µćDŌŚBCÉĻ£¬DA”ĶCAÓŚA”£
Ēó£ŗBDµÄ³¤”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĶ¼ŠĪ¶¼ŹĒÓÉĶ¬Ńł“󊔵Ċ”Ō²Č¦°“Ņ»¶Ø¹ęĀÉĖł×é³ÉµÄ£¬ĘäÖŠµŚ¢ŁøöĶ¼ŠĪÖŠŅ»¹²ÓŠ6øöŠ”Ō²Č¦£¬µŚ¢ŚøöĶ¼ŠĪÖŠŅ»¹²ÓŠ9øöŠ”Ō²Č¦£¬µŚ¢ŪøöĶ¼ŠĪÖŠŅ»¹²ÓŠ12øöŠ”Ō²Č¦£¬”£¬°““Ė¹ęĀÉÅÅĮŠ£¬ŌņµŚ¢āøöĶ¼ŠĪÖŠŠ”Ō²Č¦µÄøöŹżĪŖ( )

A. 24 B. 27 C. 30 D. 33
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
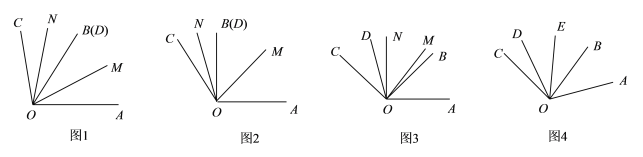
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼1£¬”ĻAOBŗĶ”ĻCOD¹²¶„µćO£¬OBŗĶODÖŲŗĻ£¬OMĪŖ”ĻAODµÄĘ½·ÖĻߣ¬ONĪŖ”ĻBOCµÄĘ½·ÖĻߣ¬”ĻAOB£½¦Į£¬”ĻCOD£½¦Ā£®
£Ø1£©ČēĶ¼2£¬Čō¦Į£½90”ć£¬¦Ā£½30”ć£¬Ōņ”ĻMON£½________£»
£Ø2£©Čō½«”ĻCODČĘOÄꏱÕėŠż×ŖÖĮĶ¼3µÄĪ»ÖĆ£¬Ēó”ĻMON£»(ÓƦĮ£¬¦Ā±ķŹ¾)
£Ø3£©ČēĶ¼4£¬Čō¦Į£½2¦Ā£¬”ĻCODČĘOÄꏱÕėŠż×Ŗ£¬×ŖĖŁĪŖ3”ć/Ćė£¬”ĻAOBČĘOĶ¬Ź±ÄꏱÕėŠż×Ŗ£¬×ŖĖŁĪŖ1”ć/Ćė(×Ŗµ½OCÓėOA¹²Ļߏ±Ķ£Ö¹ŌĖ¶Æ)£¬ĒŅOEĘ½·Ö”ĻBOD£¬ĒėÅŠ¶Ļ”ĻCOEÓė”ĻAODµÄŹżĮæ¹ŲĻµ²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĮāŠĪOABCµÄ¶„µćOŌŚ×ų±źŌµć£¬¶„µćAŌŚxÖįÉĻ£¬”ĻB=120”ć£¬OA=2£¬½«ĮāŠĪOABCČĘŌµćĖ³Ź±ÕėŠż×Ŗ105”ćÖĮOA”äB”äC”äµÄĪ»ÖĆ£¬ŌņµćB”äµÄ×ų±źĪŖ£Ø £©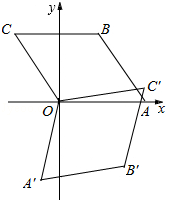
A.£Ø ![]() £¬©
£¬© ![]() £©
£©
B.£Ø© ![]() £¬
£¬ ![]() £©
£©
C.£Ø2£¬©2£©
D.£Ø ![]() £¬©
£¬© ![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com