
【题目】己知反比例函数:y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)分别求反比例函数和一次函数的解析式;
(2)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=2x+6;(2)M(x1,y1)在第三象限,N(x2,y2)在第一象限.
,一次函数的解析式为y=2x+6;(2)M(x1,y1)在第三象限,N(x2,y2)在第一象限.
【解析】试题分析:(1)由点A的坐标结合反比例函数图象上点的坐标特征即可求出反比例函数的解析式;再利用反比例函数图象上点的坐标特征求出点B的坐标,再由A、B的坐标利用待定系数法即可求出一次函数解析式;
(2)由k1的值结合反比例函数的性质即可分析出点M、N所在的象限.
试题解析:(1)∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m),
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m),
∴k1=1×8=8,
∴反比例函数的解析式为y=![]() ,
,
∵﹣4m=8,解得:m=﹣2,
∴点B的坐标为(﹣4,﹣2),
把A(1,8)、B(﹣4,﹣2)代入一次函数y=k2x+b中,
得![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=2x+6;
(2)∵反比例函数y=![]() 的图象位于一、三象限,
的图象位于一、三象限,
∴在每个象限内,y随x的增大而减小,
∵x1<x2,y1<y2,
∴M,N在不同的象限,
∴M(x1,y1)在第三象限,N(x2,y2)在第一象限.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=120°,BC=2AC.
(1)利用尺规作等腰△DBC,使点D、A在直线BC的同侧,且DB=BC,∠DBC=∠ACB(保留作图痕迹,不写画法);
(2)设(1)中所作的△DBC的边DC交AB于E点,求证:DE=3CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
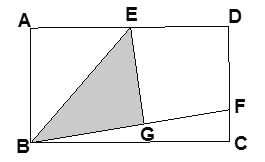
【题目】如图,在矩形![]() 中,
中, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,且点
,且点![]() 在矩形
在矩形![]() 内部,再延长
内部,再延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证: A、G、D三点在以点E为圆心,EA的长为半径的圆上;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
(1)求该抛物线的解析式及点D的坐标;
(2)连接AC,CD,BD,BC,设△AOC、△BOC、△BCD的面积分别为S1,S2和S3,求证:S3=![]() ;
;
(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时直线MN的解析式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球为关注儿童戍长的健康,实施“关注肥胖守儿童计划”,某校结全校各班肥胖儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
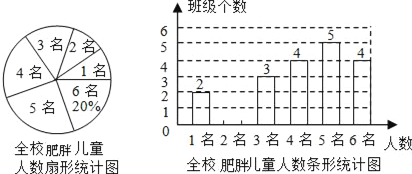
(1)全校班级个数 个 ,并将该条形统计图补充完整;
(2)为了了解肥胖儿重的饮食情况,某校决定从只有2名留守儿童的这些班级中,任选两名进行调查,请用列表法或画树形图的方法,求出所选两名肥胖儿童来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是南海中学八年级(15)班的40名学生的出生月份的调查记录:
![]()
(1)请你重新设计一张统计表,使全班同学在每个月出生人数情况一目了然;
(2)求出10月份出生的学生的频数和频率;
(3)现在是1月份,如果你准备为下个月生日的每一位同学送一份小礼物,那你应该准备多少份礼物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一条抛物线,三位学生分别说出了它的一些性质:
甲说:对称轴是直线x=2;
乙说:与x轴的两个交点距离为6;
丙说:顶点与x轴的交点围成的三角形面积等于9,请你写出满足上述全部条件的一条抛物线的解析式:_______________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com