
【题目】有20筐红萝卜,以每筐25千克为标准,超过记正不足记负来表示,记录如下:

(1)20筐红萝卜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,20筐红萝卜总计超过或不足多少千克?
(3)若该种红萝卜进价每千克为1.5元,售价每千克为3元.求这20筐红萝卜能赚多少钱?
【答案】(1)4.5千克;(2)超过12千克;(3)768元.
【解析】
(1)根据有理数的减法,可得答案;
(2)根据有理数的加法,可得答案;
(3)根据销售价格减进货价格,可得答案.
解::(1)20筐红萝卜中,最重的一筐比最轻的一筐重2.5-(-2)=4.5千克,
∴20筐红萝卜中,最重的一筐比最轻的一筐重4.5千克;
(2)1×(-2)+4×(-1.5)+2×(-1)+3×0+2×1+8×2.5
=-2-6-2+2+20
=12(千克),
∴20筐红萝卜总计超过标准重量12千克.
(3)(20×25+12)×(3-1.5)
=512×1.5
=768(元),
∴这20筐红萝卜能赚768元.
故答案为:(1)4.5千克;(2)超过12千克;(3)768元.


科目:初中数学 来源: 题型:
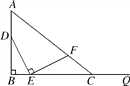
【题目】如图,AB=4,射线BQ和AB互相垂直,点D是AB上的一个动点,点E在射线BQ上,BE=![]() DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且![]() =
=![]() .连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
.连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .其中正确的是________.
.其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,在某个时刻停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶纪录如下(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)![]() 在岗亭哪个方向?距岗亭多远?
在岗亭哪个方向?距岗亭多远?
(2)若摩托车行驶每千米耗油![]() 升,每升
升,每升![]() 元,且最后返回岗亭,这一天耗油共需多少元?
元,且最后返回岗亭,这一天耗油共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
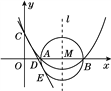
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2016年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2018年底三年累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2018年底共建设了多少万平方米廉租房.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com