
 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).
如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).分析 (1)把点C和点B分别绕点A顺时针旋转90°得到C1和B1,顺次连接即可;
(2)连接AC延长到A2使A2C=2AC,延长BC到B2,使B2C=2BC,点C2的对应点为C,顺次连接各点即可,△A2B2C的面积=$\frac{1}{2}$×底边×高.
(3)根据平行四边形的对边平行且相等,分AB、BC、AC是对角线三种情况分别写出即可.
解答 解:(1)如图所示,△AB1C1即为所作: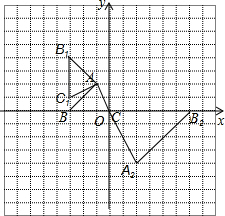
(2)如图所示△A2B2C即为所作,
由图中可知B2C为6,A2纵坐标为-4,
所以B2C2上的高为4,
故S=$\frac{1}{2}$×6×4=12;
(3)当AC为对角线时,点D坐标为(2,2);
当AB为对角线时,点D坐标为(-4,2);
当BC为对角线时,点D坐标为(-2,-2).
点评 本题主要考查了作图-旋转变换、作图-位似变换以及平行四边形的判定的知识,解答本题的关键是画位似图形的一般步骤:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
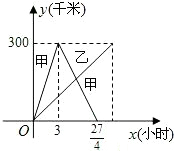 已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?
如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )| A. | 2≤k≤4 | B. | 2≤k≤5 | C. | 2≤k≤8 | D. | 5≤k≤8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
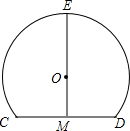 一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com